Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(8 - 7 = 1;6 - 7 = - 1;7 - 7 = 0;5 - 7 = - 2;9 - 7 = 2\)
b) +) Bình phương các độ lệch là: \({(8 - 7)^2} = 1;{(6 - 7)^2} = 1;{(7 - 7)^2} = 0;{(5 - 7)^2} = 4;{(9 - 7)^2} = 4\)
+) Trung bình cộng của bình phương các độ lệch là:
\({s^2} = \frac{{{{(8 - 7)}^2} + {{(6 - 7)}^2} + {{(7 - 7)}^2} + {{(5 - 7)}^2} + {{(9 - 7)}^2}}}{5} = 2\)

Chọn A.
Lập bảng phân bố tần số; tần suất
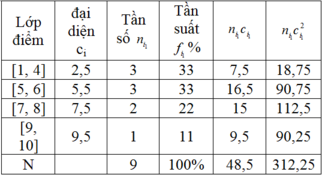
Điểm trung bình cộng của nhóm là:
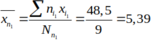

Ta có: 9 là một số lẻ nên số trung vị cùa mẫu số liệu trên là số ở vị trí chính giữa
Do đó; số trung vị của mẫu số liệu là: Me= 7
Chọn C

Chọn D.
Dãy số trên đã được sắp xếp theo thứ tự tăng dần.
Dãy số trên có 9 phần tử. Trong dãy này số đứng giữa là 7.
⇒ Số trung vị là 7.

a) Ta lập bảng tần số:
Điểm | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Tần số | 5 | 13 | 5 | 5 | 5 | 5 | 2 |
Từ đó ta thấy mốt của mẫu số liệu trên là: \({M_o} = 5\)
b) Tỉ lệ số học sinh lớp 10A đạt điểm từ 8 trở lên là: \(\frac{{5 + 5 + 2}}{{40}} = 0,3 = 30\% \)
Tỉ lệ này cho thấy số học sinh đạt điểm giỏi của lớp 10A là \(30\% \)

Chọn B.
Lập bảng phân bố tần số; tần suất
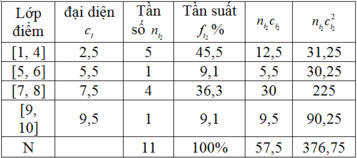
Phương sai của nhóm là
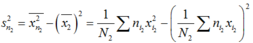
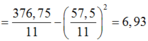

Đơn vị điều tra: một hsinh lớp 10.
Do lớp học có 22 nữ và 20 nam nên lớp có tất cả 42 học sinh . Do đó; kích thước của mẫu số liệu: 42
Chọn D

'''''''''''''F'F'S'JURSMJHYT,JTHDNHTDNMYHJFGJHTMJHTMJYT

Số trung bình cộng của mẫu số liệu trên là: \(\overline X = \frac{{1 + 1 + 3 + 6 + 7 + 8 + 8 + 9 + 10}}{9} \approx 5,9\)
Nhận xét: Quan sát mẫu số liệu trên, ta thấy nhiều số liệu có sự chênh lệch lớn so với số trung bình cộng. Vì vậy, ta không thể lấy số trung bình cộng làm đại diện cho mẫu số liệu mà ta phải chọn số đặc trưng khác thích hợp hơn.