Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(1\dfrac{4}{5}+2\dfrac{5}{7}+3\dfrac{4}{5}+4\dfrac{5}{7}\)
\(\text{=}\left(1\dfrac{4}{5}+3\dfrac{4}{5}\right)+\left(2\dfrac{5}{7}+4\dfrac{5}{7}\right)\)
\(\text{=}1+3+\left(\dfrac{4}{5}+\dfrac{4}{5}\right)+2+4+\left(\dfrac{5}{7}+\dfrac{5}{7}\right)\)
\(\text{=}10+\dfrac{8}{5}+\dfrac{10}{7}\text{=}131\dfrac{1}{35}\)

`a, 2/3 +3/4 = (8+9)/12=17/12.`
`1 1/3+4/5 = 4/3 + 4/5 = (20+12)/15=32/15`.
`=> x=2.`
`b, 5/6-1/4=(20-6)/24=7/12`.
`2 1/3-2/5= 7/3-2/5 = (35-6)/15=29/15`.
`=> x=1`.

\(1\dfrac{1}{2}x1\dfrac{1}{3}x1\dfrac{1}{4}x1\dfrac{1}{5}x1\dfrac{1}{6}x1\dfrac{1}{7}x1\dfrac{1}{8}x1\dfrac{1}{9}\)
\(=\dfrac{3}{2}x\dfrac{4}{3}x\dfrac{5}{4}x\dfrac{6}{5}x\dfrac{7}{6}x\dfrac{8}{7}x\dfrac{9}{8}x\dfrac{10}{9}\)
\(=x^7.\dfrac{3.4.5.6.7.8.9.10}{2.3.4.5.6.7.8.9}\)
\(=x^7.\dfrac{10}{2}\)
\(=5x^7\)
\(=\dfrac{3}{2}\times\dfrac{4}{3}\times\dfrac{5}{4}\times...\times\dfrac{9}{8}\times\dfrac{10}{9}=\dfrac{10}{2}=5\)

a) \(\dfrac{2}{3}+\dfrac{3}{5}=\dfrac{10}{15}+\dfrac{9}{15}=\dfrac{19}{15}\)
a) \(\dfrac{7}{12}-\dfrac{2}{7}+\dfrac{1}{12}=\dfrac{2}{3}-\dfrac{2}{7}=\dfrac{14}{21}-\dfrac{6}{21}=\dfrac{8}{21}\)

sơ đồ :
A B C M N
Tỉ số diện tích :
\(\frac{S_{MNC}}{S_{BMC}}=\frac{MN}{BM}=\frac{1}{3}\)( cùng chiều cao hạ từ C )
\(\frac{S_{BMC}}{S_{ABC}}=\frac{MC}{AC}=\frac{2}{3}\)( cùng chiều cao hạ từ B )
\(S_{MNC}=\frac{2}{3}\times\frac{1}{3}\times S_{ABC}=\frac{2}{9}\times S_{ABC}\)
\(S_{ABC}=S_{MNC}\div\frac{2}{9}=24\times\frac{9}{2}=108cm^2\)
\(S_{ABC}=108cm^2\)

\(3\dfrac{1}{5}\times\dfrac{10}{11}+1\dfrac{2}{11}\\ =\dfrac{16}{5}\times\dfrac{10}{11}+\dfrac{13}{11}\\ =\dfrac{16\times10}{5\times11}+\dfrac{13}{11}\\ =\dfrac{160}{55}+\dfrac{13}{11}\\ =\dfrac{32}{11}+\dfrac{13}{11}\\ =\dfrac{32+13}{11}\\ =\dfrac{45}{11}\)
\(5\dfrac{1}{3}:1\dfrac{2}{3}-1\dfrac{1}{5}\\ =\dfrac{16}{3}:\dfrac{5}{3}-\dfrac{6}{5}\\ =\dfrac{16}{3}\times\dfrac{3}{5}-\dfrac{6}{5}\\ =\dfrac{16\times3}{3\times5}-\dfrac{6}{5}\\ =\dfrac{48}{15}-\dfrac{6}{5}\\ =\dfrac{16}{5}-\dfrac{6}{5}\\ =\dfrac{16-6}{5}\\ =\dfrac{10}{5}\\ =2\)
\(3\dfrac{1}{5}\times\dfrac{10}{11}+1\dfrac{2}{11}\\ =\dfrac{3\times5+1}{5}\times\dfrac{10}{11}+\dfrac{1\times11+2}{11}\\ =\dfrac{16}{5}\times\dfrac{10}{11}+\dfrac{13}{11}\\ =\dfrac{160}{55}+\dfrac{13}{11}\\ =\dfrac{32}{11}+\dfrac{13}{11}\\ =\dfrac{45}{11}\)
\(5\dfrac{1}{3}:1\dfrac{2}{3}-1\dfrac{1}{5}\\ =\dfrac{5\times3+1}{3}:\dfrac{1\times3+2}{3}-\dfrac{1\times5+1}{5}\\ =\dfrac{16}{3}:\dfrac{5}{3}-\dfrac{6}{5}\\ =\dfrac{16}{3}\times\dfrac{3}{5}-\dfrac{6}{5}\\ =\dfrac{16}{5}-\dfrac{6}{5}\\ =\dfrac{10}{5}=2\)

\(\Rightarrow x+\dfrac{1}{6}=\dfrac{3}{4}\\ \Rightarrow x=\dfrac{7}{12}\)

⇔\(x\) x 1=\(\dfrac{8}{3}\)
⇔\(x\) =\(\dfrac{8}{3}\)
Vậy \(x\)=\(\dfrac{8}{3}\)
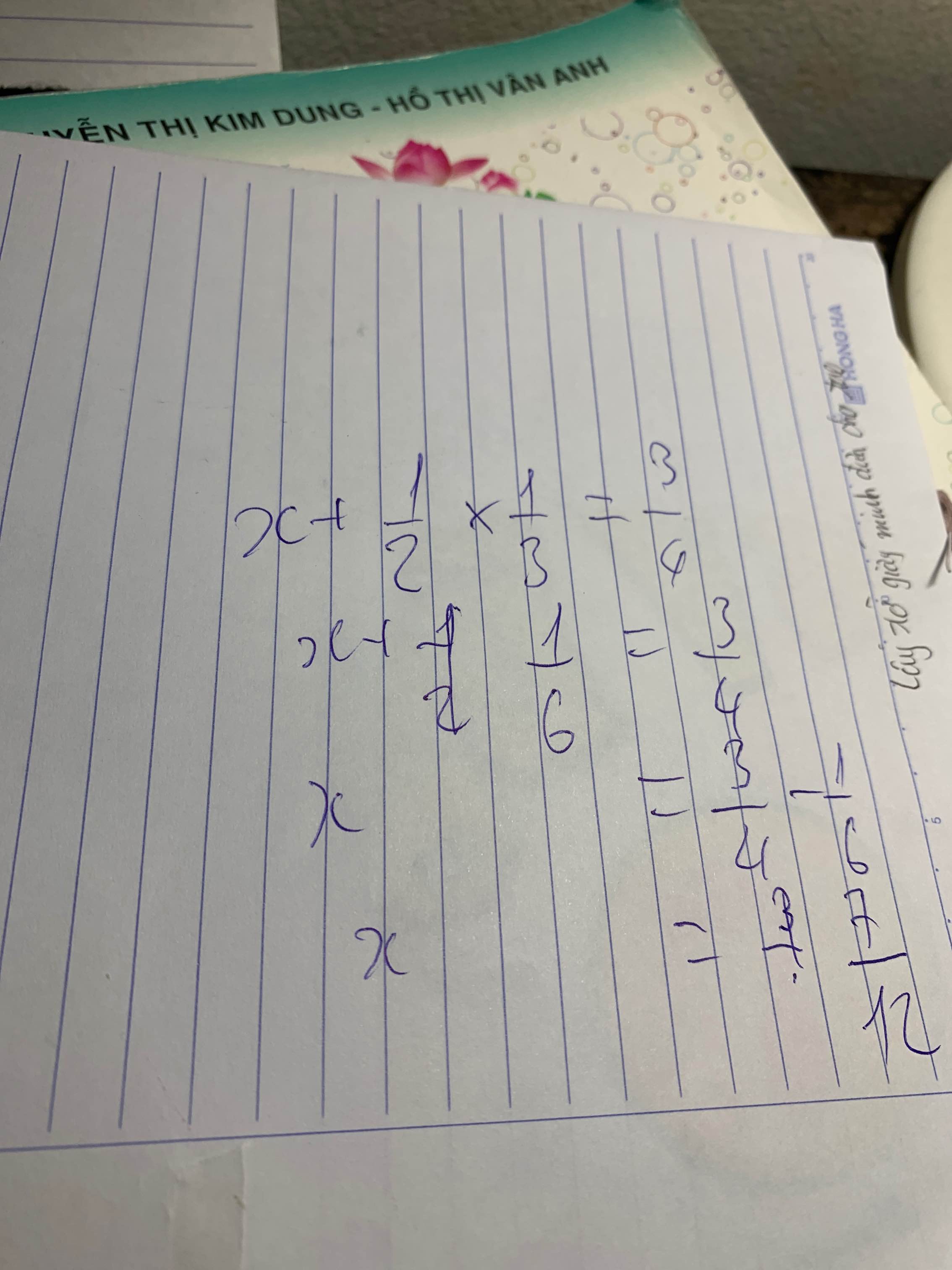
\(\dfrac{2}{3}+\dfrac{2}{6}+\dfrac{2}{12}+\dfrac{2}{24}+\dfrac{2}{48}+\dfrac{2}{96}+\dfrac{2}{192}\)
\(=\dfrac{2}{3}\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+\dfrac{1}{32}+\dfrac{1}{64}\right)\)
\(=\dfrac{2}{3}\cdot\dfrac{63}{64}=\dfrac{21}{32}\)
A = \(\dfrac{2}{3}\) + \(\dfrac{2}{6}\) + \(\dfrac{2}{12}\) + \(\dfrac{2}{24}\) + \(\dfrac{2}{48}\) + \(\dfrac{2}{96}\) + \(\dfrac{2}{192}\)
2 x A = \(\dfrac{4}{3}\) + \(\dfrac{2}{3}\) + \(\dfrac{2}{6}\) + \(\dfrac{2}{12}\) + \(\dfrac{2}{24}\) + \(\dfrac{2}{48}\) + \(\dfrac{2}{96}\)
2 x A - A = \(\dfrac{4}{3}\) + \(\dfrac{2}{3}\) + \(\dfrac{2}{6}\) + ... + \(\dfrac{2}{96}\) - (\(\dfrac{2}{3}\) + \(\dfrac{2}{6}\) + ... + \(\dfrac{2}{96}\) + \(\dfrac{2}{192}\))
A x (2 - 1) = \(\dfrac{4}{3}\) + \(\dfrac{2}{3}\) + \(\dfrac{2}{6}\) + ... + \(\dfrac{2}{96}\) - \(\dfrac{2}{3}\) - \(\dfrac{2}{6}\) - ... - \(\dfrac{2}{96}\) - \(\dfrac{2}{192}\)
A = (\(\dfrac{4}{3}\) - \(\dfrac{2}{192}\))+ (\(\dfrac{2}{3}\) - \(\dfrac{2}{3}\)) + (\(\dfrac{2}{6}\) - \(\dfrac{2}{6}\)) + ... + (\(\dfrac{2}{96}\) - \(\dfrac{2}{96}\))
A = \(\dfrac{4}{3}\) - \(\dfrac{2}{192}\) + 0 + 0 + 0 + ... + 0
A = \(\dfrac{127}{96}\)