Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án nè:
Đặt A=\(\dfrac{1}{3}-\dfrac{2}{3^2}+\dfrac{3}{3^3}-\dfrac{4}{3^4}+...+\dfrac{99}{3^{99}}-\dfrac{100}{3^{99}}\)
3A=\(\dfrac{1}{1}-\dfrac{2}{3}+\dfrac{3}{3^2}-\dfrac{4}{3^3}+...+\dfrac{99}{3^{98}}-\dfrac{100}{3^{99}}\)
3A+A=\(\left(\dfrac{1}{1}-\dfrac{2}{3}+\dfrac{3}{3^2}-\dfrac{4}{3^3}+...+\dfrac{99}{3^{98}}-\dfrac{100}{3^{99}}\right)+\left(\dfrac{1}{3}-\dfrac{2}{3^2}+\dfrac{3}{3^3}-\dfrac{4}{3^4}+...+\dfrac{99}{3^{99}}-\dfrac{100}{3^{100}}\right)\)
4A=\(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}-\dfrac{1}{3^{100}}\)
4A bé hơn(sorry tớ không thấy dấu bé hơn)\(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\)
Đặt B=\(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3^2}-\dfrac{1}{3^3}+...+\dfrac{1}{3^{99}}\)
3B=\(3-1+\dfrac{1}{3}-\dfrac{1}{3^2}+...+\dfrac{1}{3^{98}}\)
4B=\(3-\dfrac{1}{3^{99}}\) bé hơn 3 \(\Rightarrow\)B bé hơn \(\dfrac{3}{4}\)
\(\Rightarrow\) 4A bé hơn\(\dfrac{3}{4}\Rightarrow\)A bé hơn \(\dfrac{3}{16}\)
Tick cho mình nha , ngồi đánh máy tính mỏi cả mắt lun
Chúc học tốt![]()

Xét thừa số tổng quát: \(n!=1.2.3...n\)
Ta có:
\(L=\dfrac{1}{2!}+\dfrac{2}{3!}+\dfrac{3}{4!}+...+\dfrac{99}{100!}\)
\(L=\dfrac{2-1}{2!}+\dfrac{3-1}{3!}+\dfrac{4-1}{4!}+...+\dfrac{100-1}{100!}\)
\(L=\dfrac{2-1}{1.2}+\dfrac{3-1}{1.2.3}+\dfrac{4-1}{1.2.3.4}+...+\dfrac{100-1}{1.2.3...100}\)
\(L=1-\dfrac{1}{1.2}+\dfrac{1}{1.2}-\dfrac{1}{1.2.3}+\dfrac{1}{1.2.3}-\dfrac{1}{1.2.3.4}+...+\dfrac{1}{1.2.3....99}-\dfrac{1}{1.2.3...100}\)
\(L=1-\dfrac{1}{1.2.3....100}< 1\left(đpcm\right)\)
Xét thừa số tổng quát: n ! = 1.2.3 ... nn!=1.2.3 ...n
Ta có:
L = 1 2 !+ 2 3 !+ 3 4 !+ . . . + 99 100 !L=12!+23!+34!+...+99100!
L = 2 - 1 2 !+ 3 - 1 3 !+ 4 - 1 4 !+ . . . + 100 - 1 100 !L=2- -12!+3- -13!+4- -14!+...+100- -1100!
L = 2 - 1 1.2+ 3 - 1 1.2.3+ 4 - 1 1.2.3.4+ . . . + 100 - 1 1.2.3 ... 100L=2−11.2+3−11.2.3+4−11.2.3.4+...+100−11.2.3...100
L = 1 - 1 1.2+ 1 1.2- 1 1.2.3+ 1 1.2.3- 1 1.2.3.4+ . . . + 1 1.2.3 .... 99- 1 1.2.3 ... 100L=1−11.2+11.2−11.2.3+11.2.3−11.2.3.4+...+11.2.3....99−11.2.3 ... 100
L = 1 - 1 1.2.3 .... 100<1(đpcm)

Ta có :
\(\dfrac{a}{b}=\dfrac{a.\left(b+d\right)}{b.\left(b+d\right)}=\dfrac{ab+bd}{b^2+bd}\)
\(\dfrac{a+c}{b+d}=\dfrac{b\left(a+c\right)}{b\left(b+d\right)}=\dfrac{ab+bc}{b^2+bd}\)
Ta so sánh :
\(\dfrac{ab+bd}{b^2+bd}\) và \(\dfrac{ab+bc}{b^2+bd}\)
Vì cùng mẫu nên ta chỉ so sánh :
\(ab+bd\) và \(ab+bc\)
\(\Rightarrow\) Ta tiếp tục so sánh :
\(bd\) và bc thì ta có : bd < bc (1)
Từ 1, suy ra :
\(\dfrac{a}{b}< \dfrac{a+c}{b+c}\)
Mà \(\dfrac{a}{b}< \dfrac{c}{d}\)
Suy ra : \(\dfrac{a}{b}< \dfrac{a+c}{b+d}< \dfrac{c}{d}\) (đpcm)

a) Giải
Đặt \(M=\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}...\dfrac{98}{99}\)
\(\Rightarrow A< A.M\)
hay \(A< \left(\dfrac{1}{2}.\dfrac{3}{4}.\dfrac{5}{6}...\dfrac{99}{100}\right).\left(\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}...\dfrac{98}{99}\right)\)
\(\Rightarrow A< \dfrac{1}{2}.\dfrac{2}{3}.\dfrac{3}{4}.\dfrac{4}{5}.\dfrac{5}{6}.\dfrac{6}{7}...\dfrac{98}{99}.\dfrac{99}{100}\)
\(\Leftrightarrow A< \dfrac{1.2.3.4.5.6...98.99}{2.3.4.5.6.7...99.100}\)
\(\Rightarrow A< \dfrac{1}{100}< \dfrac{1}{10}\)
Vậy \(A< \dfrac{1}{10}\)
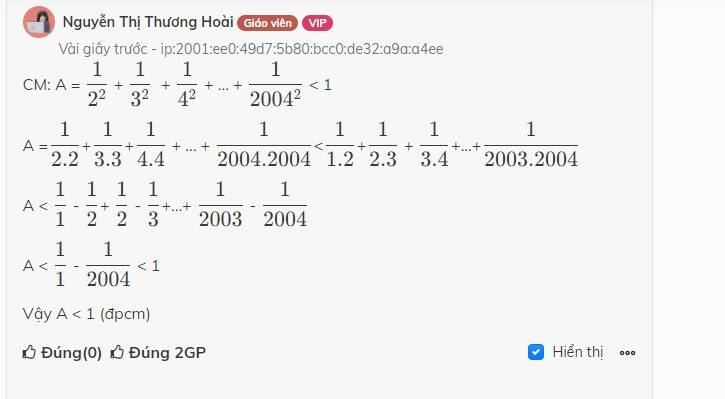
đúng
Đúng. Vì khi ta quy đồng lên ta có
1/299=1.2/299.2=2/2100
Vậy 2/2100=1/299
Chúc bạn học tốt!