Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi: \(\frac{1}{2}\) giờ = 30 phút
Thời gian người đó đi hết quãng đường AB là:
1 giờ 15 phút + 30 phút + 25 phút = 2 giờ 10 phút
Xe máy khởi hành từ A lúc 7 giờ 45 phút đến B lúc:
7 giờ 45 phút + 2 giờ 10 phút = 9 giờ 55 phút

ta có : _ 4 giờ 30 phút = 9/2 giờ
_ 2 giờ 15 phút = 9/4 giờ
Trong 1 giờ, vòi A chảy được số phần bể nước là:
1 : 9/2 = 2/9 ( bể nước )
Trong 1 giờ, vòi B chảy được số phần bể nước là:
1 : 9/4 = 4/9 ( bể nước )
Trong 1 giờ, cả 2 vòi chảy được số phần bể nước là:
2/9 + 4/9 = 6/9 ( bể nước )
Thời gian để cả 2 vòi chayw đầy bể là:
1 : 6/9 = 9/6 ( giờ )
Đáp số: 9/6 giờ hay 1 giờ 30 phút![]()

Đáp án A.
Ta có:
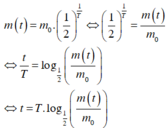
Theo giả thiết ta có:
T = 1602(năm), m 0 = 1 g r a m , m t = 0.5 g r a m
Áp dụng công thức ta có khoảng thời gian cần tìm là:
t = T . log 1 2 m t m 0 = 1602. log 1 2 0.5 1 = 1602. log 1 2 1 2 = 1602
Vậy sau 1602 năm thì 1gram chất phóng xạ này bị phân ra còn lại 0.5 gram

2.
Gọi quãng đường cần tìm là s.---> vận tốc Xuân= s/12,
--> vận tốc Hạ=s/10
thời gian Xuân gặp Hạ: 50/(s/12)= (s-50)/(s/10)
50x12/s= (s-50)x10/s
50x12=10s-500
---> s = (500+50x12)/10= 110
quãng đường giữa nhà hai bạn là 110m
4.
Khi ngược dòng 1 giờ ta đi được số phần quãng sông là:
1 : 8 = 1/8 (quãng sông)
Khi xuôi dòng 1 giờ ta đi được số phần quãng sông là:
1 : 4 = 1/4 (quãng sông)
Bèo trôi theo ta về 1 giờ trôi được số phần quãng sông là:
(1/4 - 1/8) : 2 = 1/16 (quãng sông)
Bèo trôi theo ta về cập bến sau số giờ là:
1 : 1/16 = 16 (giờ)
Đ/s: 16 giờ

▲\(\frac{11\frac{1\frac{1}{1\frac{1}{1^{ }}}}{1}}{20\frac{1}{1\frac{1}{1\frac{1}{1\frac{1}{1}}}}1}\)
Số lượng nước cả 2 chảy là :
\(\frac{1}{3}+\frac{1}{4}=\frac{7}{12}\) bể
Số lượng nước còn lại chiếm số phần bể là :
\(\frac{7}{12}-\frac{1}{6}=\frac{5}{12}\) bể
Đáp số : \(\frac{5}{12}\) bể

a) Sau 2 giờ, vòi nước chảy được:
2/7+2/7=4/7 ( bể)
b) Nếu đã dùng hết lượng nước bằng 1/3 bể thì nước còn lại chiếm:
4/7-1/3=5/21( bể)
Đáp số: a) 4/7 bể
b) 5/21 bể
Gọi ∆ N 1 là số hạt β - được phóng ra trong khoảng thời gian ∆ t 1 kể từ thời điểm ban đầu.
Ta có
∆ N 1 = N 01 - N 1 = N 01 1 - e - k ∆ t 1
với N 01 là số hạt phóng xạ β - ban đầu.
Sau 3 giờ, số nguyên tử còn lại trong chất phóng xạ là N 02 = N 01 . e - 3 k .
Kể từ thời điểm này, trong khoảng thời gian ∆ t 2 thì số hạt β - tạo thành là
∆ N 2 = N 02 - N 01 = N 02 1 - e - k ∆ t 2
Cho ∆ t 1 = ∆ t 2 = 1 phút thì theo giả thiết, ta có ∆ N 1 = 960; ∆ N 2 = 120. Khi đó
∆ N 1 ∆ N 2 = e - 3 k ⇔ 120 960 = e - 3 k ⇔ 8 - 1 = e - 3 k ⇔ k = ln 2
Vậy T = k ln 2 = 1 (giờ) là chu kỳ bán rã của chất phóng xạ.
Đáp án B