Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có; log245= log2( 32. 5) = 2log23+ log25
= 2a+ log23.log35= 2a+ ab
Do đó, log245= 2a+ ab.
Chọn D.

a) Ta có:
a = log 3 15 = log 3 ( 3 , 5 ) = log 3 3 + log 3 5 = 1 + log 3 5
Suy ra log 3 5 = a – 1
b = log 3 10 = log 3 ( 2 , 5 ) = log 3 2 + log 3 5
Suy ra log 3 2 = b − log 3 5 = b − (a − 1) = b – a + 1
Do đó:
log 3 50 = log 3 0 , 5 ( 2 . 52 ) = 2 log 3 2 + 4 log 3 5 = 2 (b – a + 1) + 4(a − 1) = 2a + 2b − 2
b) Ta có:
log 140 63 = log 140 ( 32 . 7 ) = 2 log 140 3 + log 140 7
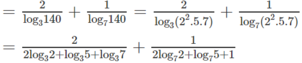
Từ đề bài suy ra:
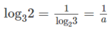
log 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
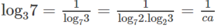
Vậy
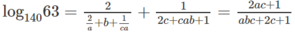

Ta có:
log 140 63 = log 140 3 2 . 7 = 2 log 140 3 + log 140 7
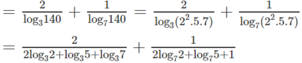
Từ đề bài suy ra:
![]()
loh 0 , 5 π . log 7 5 = log 7 2 . log 2 3 . log 35 = cab
![]()
Vậy
![]()
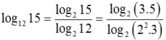
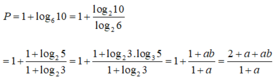
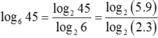

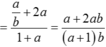
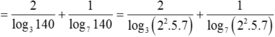
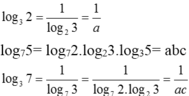
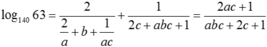



Chọn D.
Ta có: log245 = log2( 32. 5) = 2log23 + log25
= 2a + log23.log35 = 2a + ab