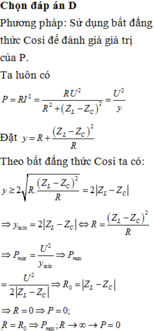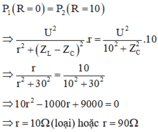Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

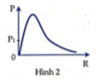
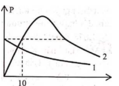
\(U_C=I.Z_C=\dfrac{U.Z_C}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}.\omega C}=\dfrac{U}{\sqrt{\omega^2.C^2.R^2+(\omega^2.LC-1)^2}}\)
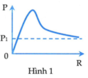
Suy ra khi \(\omega=0\) thì \(U_C=U\) \(\Rightarrow (1)\) là \(U_C\)
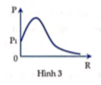
\(U_L=I.Z_L=\dfrac{U.Z_L}{\sqrt{R^2+(Z_L-Z_C)^2}}=\dfrac{U.\omega L}{\sqrt{R^2+(\omega.L-\dfrac{1}{\omega C})^2}}=\dfrac{U.L}{\sqrt{\dfrac{R^2}{\omega^2}+(L-\dfrac{1}{\omega^2 C})^2}}\)(chia cả tử và mẫu cho \(\omega\))
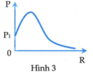
Suy ra khi \(\omega\rightarrow \infty\) thì \(U_L\rightarrow U\) \(\Rightarrow (3) \) là \(U_L\)
Vậy chọn \(U_C,U_R,U_L\)

Đáp án D
Phương pháp: Sử dụng bất đẳng thức Cosi để đánh giá giá trị của P
Ta luôn có: P = R . I 2 = R U 2 R 2 + Z L − Z C 2 = U 2 y . Đặt y = R + Z L − Z C 2 R
Theo bất đẳng thức Cosi ta có:
y ≥ 2 R . Z L − Z C 2 R = 2 Z L − Z C ⇒ y min = 2 Z L − Z C ⇔ R = Z L − Z C 2 R ⇒ P max = U 2 y min ⇒ P max = U 2 2 Z L − Z C ⇒ R 0 = Z L − Z C ⇒ R = 0 ⇒ P = 0 ; R = R 0 ⇒ P max R → ∞ → P = 0

Khi trong mạch xảy ra cộng hưởng thì ω = ${\omega _0} = \dfrac{1}{{\sqrt {LC} }}$.

1. Cường độ dòng điện cùng pha với điện áp -> \(Z_L=Z_C\)
Nếu nối tắt tụ C thì mạch chỉ còn R nối tiếp với L.
\(\tan\varphi=\frac{Z_L}{R}=\tan\frac{\pi}{3}=\sqrt{3}\Rightarrow Z_L=\sqrt{3}.50=50\sqrt{3}\Omega\)
\(\Rightarrow Z_C=50\sqrt{3}\Omega\)
2. Cuộn dây phải có điện trở R
Ta có giản đồ véc tơ
Ud Uc Um 120 120 Ur 45 0
Từ giản đồ ta có: \(U_C=\sqrt{120^2+120^2}=120\sqrt{2}V\)
\(U_R=120\cos45^0=60\sqrt{2}V\)
Cường độ dòng điện: \(I=\frac{U_C}{Z_C}=\frac{120\sqrt{2}}{200}=0,6\sqrt{2}V\)
Công suất: \(P=I^2R=I.U_R=0,6\sqrt{2}.60\sqrt{2}=72W\)

trong trường hợp ban đầu
điện áp R cực đại nên tại f1 xảy ra hiện tượng cộng hưởng
\(Z_L=Z_C\)
\(LC=\frac{1}{\omega^2_1}\)
Trong trường hợp sau thì điện áp AM không đổi khi thay đổi R, lúc cố định tần số nghĩa là cảm kháng và dung kháng đều cố định
như vậy thì chỉ có trường hợp duy nhất là Uam bằng với U
Khi đó
\(Z_{LC}=Z_L=Z_C-Z_L\)
\(Z_C=2Z_L\)
\(LC=\frac{1}{2\omega^2_2}\)
Suy ra
\(\omega^2_1=2\omega^2_2\)
\(f_1=\sqrt{2}f_2\)

+ Ta có:
![]()
+ Lúc đầu, chưa nối tắt cuộn dây công suất trên mạch là:
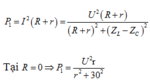
+ Lúc sau, khi nối tắt cuộn dây công suất trên mạch là:
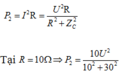
+ Vì
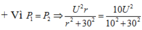
![]()
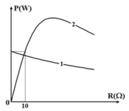
+ Từ đồ thị nhận thấy công suất trên toàn mạch khi chưa nối tắt cuộn dây có giá trị lớn nhất phải ứng với R < 0 và theo bất đang thức Cô-si ta có:
![]()
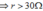
Chọn r = 90 Chọn B

Chọn đáp án A.
Ta có: ![]()
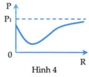
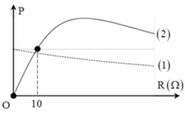
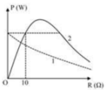
Đồ thị (1) mạch RLrC có đồ thị công suất toàn mạch
P
1
theo R chỉ là một đường nghịch biến nên ![]()
Đồ thị (2) mạch RC có đồ thị công suất toàn mạch P 2 theo R
Nhìn vào đồ thị ta thấy P 1 ( R = 0 ) = P 2 ( R = 10 )
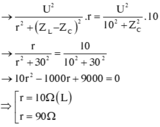
Cẩn thận đối chiếu điều kiên (*) để loại nghiệm