Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.







dùng ông thức hạ bậc
cos2a=\(\dfrac{1+cos2a}{2}\)
pt<=>1+cos(4x+\(\dfrac{2\Pi}{3}\))-3sin(2x+\(\dfrac{5\Pi}{6}\))+1=0
<=>-\(\dfrac{1}{2}\)cos4x-\(\dfrac{\sqrt{3}}{2}\)sin4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x-\(\dfrac{3}{2}\)cos2x+2=0
<=>(-\(\dfrac{1}{2}\)cos4x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)+(-\(\sqrt{3}\)sin2x.cos2x-\(\dfrac{3}{2}\)cos2x)=0
<=>[-\(\dfrac{1}{2}\)(1-2sin22x)+\(\dfrac{3\sqrt{3}}{2}\)sin2x+2)-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0
<=>(sin22x+\(\dfrac{3\sqrt{3}}{2}\)sin2x+\(\dfrac{3}{2}\))-cos2x.(\(\sqrt{3}\)sin2x+\(\dfrac{3}{2}\))=0
<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x+\(\sqrt{3}\))-cos2x.(sin2x+\(\dfrac{\sqrt{3}}{2}\))=0
<=>(sin2x+\(\dfrac{\sqrt{3}}{2}\))(sin2x-cos2x+\(\sqrt{3}\))=0
tới đây bạn tự giải nhé


cau 12:
gọi E là trung điểm AB \(\Rightarrow\)MẸ//BC ; và EN// AC do do ME=BD/2 ;NE= AC/2
\(\Rightarrow\left[\widehat{BD;AC}\right]=\left[\widehat{ME;EN}\right]=90^0\)
\(\Delta MEN\)vuông tại E\(\Rightarrow MN^2=ME^2+NE^2=\left(\dfrac{3a}{2}\right)^2+\left(\dfrac{a}{2}\right)^2=\left(\dfrac{10a^2}{4}\right)\Rightarrow MN=\dfrac{a\sqrt{10}}{2}\)
chọn đáp án A
vẽ hình ở ngoài rồi dán vào ko biết tại sao nó lại thụt xuống dưới![]()

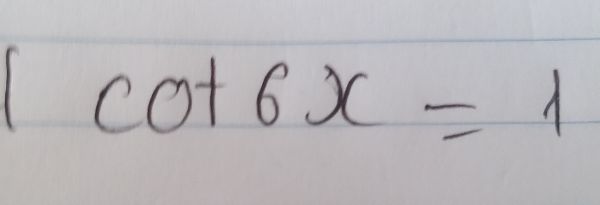

 giúp t với ạ
giúp t với ạ
 giúp mình với ạ
giúp mình với ạ
 p nào làm giúp mk với ạ
p nào làm giúp mk với ạ