
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
\(3333^{4444}=3.1111^{4.1111}=\left(3.1111^4\right)^{1111}=3^4\)
\(4444^{3333}=4.1111^{3.1111}=\left(4.1111\right)^{1111}=4^3\)
vì \(3^4=81\)
\(4^3=64\)
\(\Rightarrow3^4>4^3\)
Vậy \(3333^{4444}>4444^{3333}\)

a: Ta có: \(AN=NB=\dfrac{AB}{2}\)
\(AM=MC=\dfrac{AC}{2}\)
mà AB=AC
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC
\(\widehat{NBC}=\widehat{MCB}\)(ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB
b: Xét ΔABC có
AD,BM,CN là các đường trung tuyến
AD,BM,CN đồng quy tại G
Do đó: G là trọng tâm của ΔABC
=>\(AG=2GD\)
mà AG=GE
nên GE=2GD
=>D là trung điểm của GE
=>DG=DE
c: Ta có: ΔABC cân tại A
mà AD là đường trung tuyến
nên AD\(\perp\)BC
Xét ΔCGE có
CD là đường cao
CD là đường trung tuyến
Do đó: ΔCGE cân tại C
d: Xét ΔABC có
BM là đường trung tuyến
G là trọng tâm
Do đó: \(BG=\dfrac{2}{3}BM=10\left(cm\right)\)
D là trung điểm của BC
=>DB=DC=BC/2=8(cm)
ΔGDB vuông tại D
=>\(GD^2+DB^2=GB^2\)
=>\(GD^2=10^2-8^2=36\)
=>\(GD=\sqrt{36}=6\left(cm\right)\)
\(\Leftrightarrow AG=2\cdot GD=12\left(cm\right)\)


a)Xét ΔBAD va ΔBHD
Có BA=BH;BD là cạnh chung;gocABD=goc HBD→ΔBAD=ΔBHD(c-g-c)
→góc BAD=gocBHD(góc tương ứng)
→góc BAD=gocBAH=90 độ→DH vuông góc với BC
b)ΔBAD=ΔBHD(phần a)→gocADB=gocHDB
→ADB=HDB=110 chia 2=55 độ
Xét ΔABD .Có góc A + gocABD + goc BDA=180 do
→goc ABD=180-90-55=35 do


a: Xét ΔAHE có
AM là đường cao
AM là đường trung tuyến
DO đó: ΔAHE cân tại A
hay AH=AE
b: Xét ΔAKI và ΔAHI có
AK=AH
\(\widehat{KAI}=\widehat{HAI}\)
AI chung
Do đó: ΔAKI=ΔAHI
Suy ra: \(\widehat{AKI}=\widehat{AHI}=90^0\)
hay IK//AB
c: Ta có: IK=IH
mà IK<IC
nên IH<IC

Ở đây dấu * mik vẽ trong fx là như vầy \(\circledast\)
Xét phép trừ thứ hai: \(\overline{\circledast\circledast\circledast}-\overline{\circledast\circledast}=\circledast\) suy ra số bị trừ có dạng \(\overline{10\circledast}\), do đó bằng 100 (vì chữ số đơn vị của số bị trừ là chữ số 0 thêm vào để tìm các chữ số thập phân của thương).
Đặt số chia, thương và tích riêng thứ nhất theo thứ tự là \(\overline{ab};\overline{c,deg};\overline{mn}.\)
Ta thấy 10: \(\overline{ab}=\overline{0,deg}\) nên \(10000=\overline{ab}.\overline{deg}.\)
Chú ý rằng \(d\ne0\) (vì nếu d = 0 thì \(\overline{ab}.\overline{eg}< 10000\) ), \(g\ne0\) (vì nếu g = 0 thì thương đã dừng lại ở e), \(\overline{deg}\) là ước của 10 000 và có ba chữ số. Suy ra \(\overline{deg}\) bằng 53 =125 hoặc 54 = 625. Tương ứng \(\overline{ab}=80\) hoặc 16.

Trường hợp \(\overline{ab}=80\) thì \(\overline{mn}=80\), trái với \(80+10=\circledast\circledast\circledast\) (số bị chia), loại.
Trường hợp \(\overline{ab}=16\) thì \(c=6,\overline{mn}=96,\) số bị chia là 96 + 10 = 106
Ta có: \(106:16=6,625\) và 


minh co gang lam tung buoc nho cho ban hieu.
\(4-\left(x-\frac{1}{2}\right)-3\left(5-x\right)=0\)
{nhan pp pha ngoac
\(4-x+\frac{1}{2}-3.5+3.x=0\)
{gom cac so hang, hang so chuyen ben tay phai}
\(\left(3x-x\right)=3.5-4-\frac{1}{2}=15-4-\frac{1}{2}=11-\frac{1}{2}=\frac{21}{2}\)
\(2x=\frac{21}{2}\Rightarrow x=\frac{21}{2}:\frac{2}{1}=\frac{21}{2}.\frac{1}{2}=\frac{21}{4}\)
\(x=\frac{21}{4}\)



 ai cứu em với ạ em cần nộp trc 7h10 ạ
ai cứu em với ạ em cần nộp trc 7h10 ạ
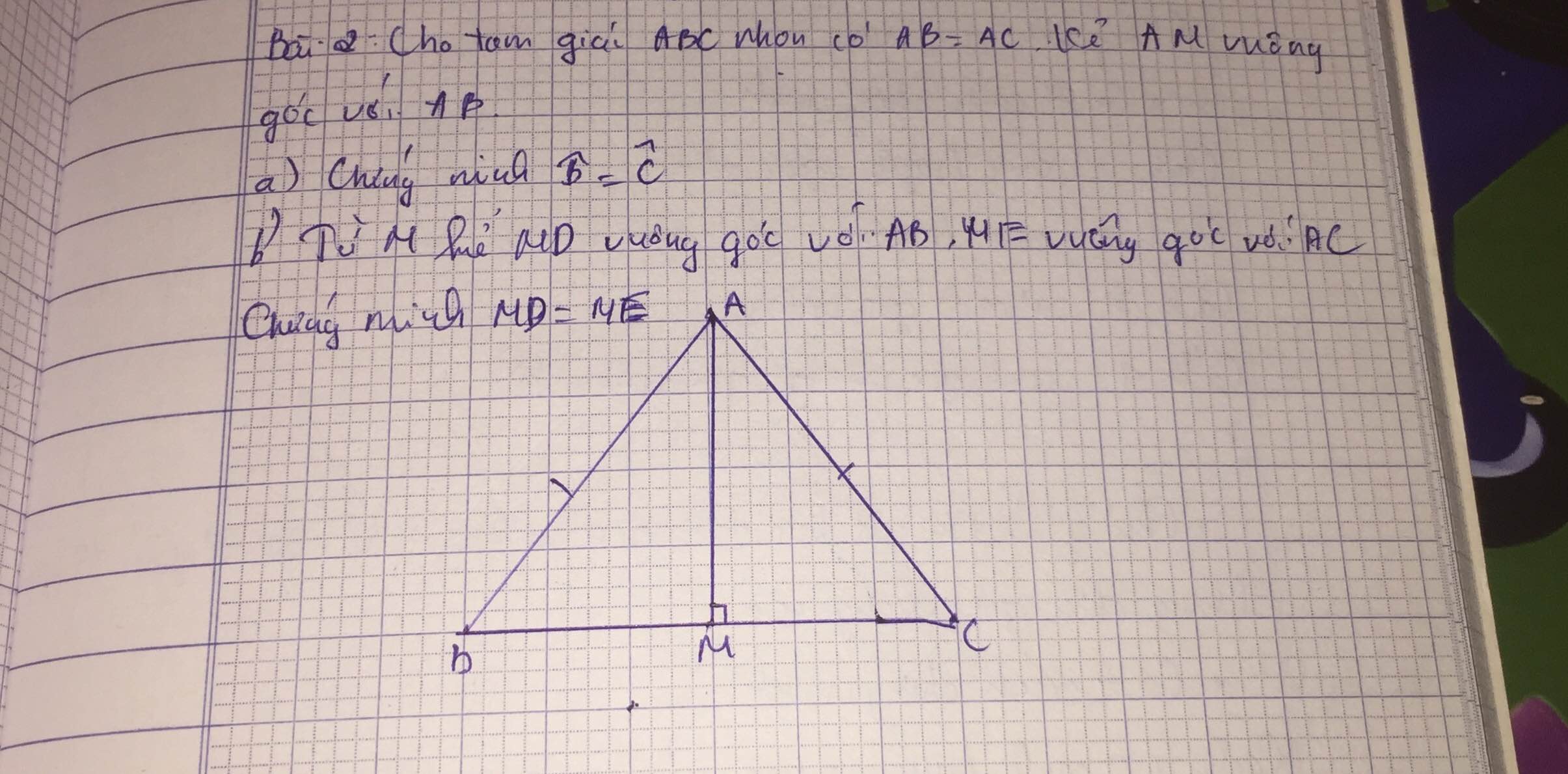
a. ta có : AB = AC ( gt )
=> ABC cân
=> góc B = góc C
b. xét 2 tam giác AMD và AMC có
A: góc chung ( ABC cân, AM là đường cao cũng là phân giác )
AM cạnh chung
Vậy....
a) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\left(gt\right)\)
\(AM\) chung
\(\widehat{AMB}=\widehat{AMC}\left(AM\perp BC\right)\)
\(\Rightarrow\Delta AMB=\Delta AMC\)(cạnh huyền-cạnh góc vuông)
\(\Rightarrow\widehat{ABM}=\widehat{ACM}\) hay \(\widehat{B}=\widehat{C}\)
b)Từ \(\Delta AMB=\Delta AMC\left(cmt\right)\)
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\)
Xét \(\Delta AMD\) và \(\Delta AME\) có:
\(\widehat{ADM}=\widehat{AEM}\left(MD\perp AB;ME\perp AC\right)\)
\(AM\) chung
\(\widehat{DAM}=\widehat{EAM}\left(\widehat{BAM}=\widehat{CAM}\right)\)
\(\Rightarrow\Delta ADM=\Delta AEM\) (góc nhọn-cạnh góc vuông)
\(\Rightarrow MD=ME\)