
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a.
$=\frac{3}{5}-\frac{7}{4}=\frac{12-35}{20}=\frac{-23}{20}$
b.
$=-(2+\frac{5}{8})=-\frac{21}{8}$
c.
$=-(\frac{1}{8}+\frac{5}{9})=-\frac{9+8.5}{8.9}=\frac{-49}{72}$
d.
$=\frac{6}{13}-\frac{14}{39}=\frac{18}{39}-\frac{14}{39}=\frac{4}{39}$
e.
$=\frac{-3}{4}+\frac{5}{7}=\frac{5}{7}-\frac{3}{4}$
$=\frac{20-21}{7.4}=\frac{-1}{28}$

Bài 5
1) x ∈ Ư(18) = {1; 2; 3; 6; 9; 18}
x ∈ B(4) = {0; 4; 8; 12; 16; 20; ...}
Vậy không tìm được x thỏa mãn đề bài
2) x ∈ Ư(20) = {1; 2; 4; 5; 10; 20}
x ∈ B(2) = {0; 2; 4; 6; 8; 10; 12; 14; 16; 18; 20; ...}
⇒ x ∈ {2; 4; 10; 20}
3) x ∈ B(12) = {0; 12; 24; 36; 48; ...; 96; 108; ...}
Mà 30 ≤ x ≤ 100
⇒ x ∈ {36; 48; ...; 96}
4) x ∈ Ư(150) = {1; 2; 3; 5; 6; 10; 15; 25; 30; 50; 75; 150}
Mà x ≤ 50
⇒ x ∈ {1; 2; 3; 5; 6; 10; 15; 25; 30; 50}
5) 70 ⋮ x và 168 ⋮ x
⇒ x ∈ ƯC(70; 168)
Ta có:
70 = 2.5.7
168 = 2³.3.7
⇒ ƯCLN(70; 168) = 2.7 = 14
⇒ x ∈ ƯC(70; 168) = Ư(14) = {1; 2; 7; 14}
Mà x > 10
⇒ x = 14
6) Ta có:
(1995 + 2005 + x) ⋮ 5
1995 ⋮ 5
2005 ⋮ 5
⇒ x ⋮ 5
⇒ x ∈ B(5) = {0; 5; 10; 15; 20; 25; 30; 35; 40; ...}
Mà 23 < x ≤ 35
⇒ x ∈ {25; 30; 35}
Bài 6
1) Do 17x2y chia hết cho 2 và 5 nên y = 0
⇒ Số đã cho có dạng: 17x20
Để 17x20 chia hết cho 3 thì (1 + 7 + x + 2 + 0) ⋮ 3
⇒ (10 + x) ⋮ 3
⇒ x ∈ {2; 5; 8}
Vậy x ∈ {2; 5; 8}; y = 0
2) Do 234xy chia hết cho 2 và 5 nên y = 0
⇒ Số đã cho có dạng: 234x0
Để 234x0 chia hết cho 9 thì (2 + 3 + 4 + x + 0) ⋮ 9
⇒ (9 + x) ⋮ 9
⇒ x ∈ {0; 9}
Vậy x ∈ {0; 9}; y = 0
3) Do 4x6y chia hết cho 2 và 5 nên y = 0
Mà x - y = 4
⇒ x = 4 + y
⇒ x = 4
Vậy x = 4; y = 0
4) Do 57x2y chia hết cho 5 nhưng không chia hết cho 2 nên y = 5
⇒ Số đã cho có dạng 57x25
Để 57x25 chia hết cho 9 thì (5 + 7 + x + 2 + 5) ⋮ 9
⇒ (19 + x) ⋮ 9
⇒ x = 8
Vậy x = 8; y = 5


\(a,-\dfrac{5}{7}+1+\dfrac{30}{-7}\le x\le-\dfrac{1}{6}+\dfrac{1}{3}+\dfrac{5}{6}\\ \dfrac{-5+1.7-30}{7}\le x\le\dfrac{-1+1.2+5}{6}\\ -\dfrac{28}{7}\le x\le\dfrac{6}{6}\\ -4\le x\le1\\ Vậy:x\in\left\{-4;-3;-2;-1;0;1\right\}\)
\(b,\dfrac{-8}{13}+\dfrac{7}{17}+\dfrac{21}{13}\le x\le-\dfrac{9}{14}+3+\dfrac{5}{-14}\\ \left(\dfrac{21}{13}-\dfrac{8}{13}\right)+\dfrac{7}{17}\le x\le\left(-\dfrac{9}{14}-\dfrac{5}{14}\right)+3\\ 1+\dfrac{7}{17}\le x\le-1+3\\ 1\dfrac{7}{17}\le x\le2\\ Vậy:x=2\)

Lời giải:
$\frac{1}{50}> \frac{1}{100}$
$\frac{1}{51}> \frac{1}{100}$
.....
$\frac{1}{98}> \frac{1}{100}$
$\frac{1}{99}> \frac{1}{100}$
$\Rightarrow S> \underbrace{\frac{1}{100}+\frac{1}{100}+...+\frac{1}{100}}_{50}=\frac{1}{100}.50=\frac{1}{2}$

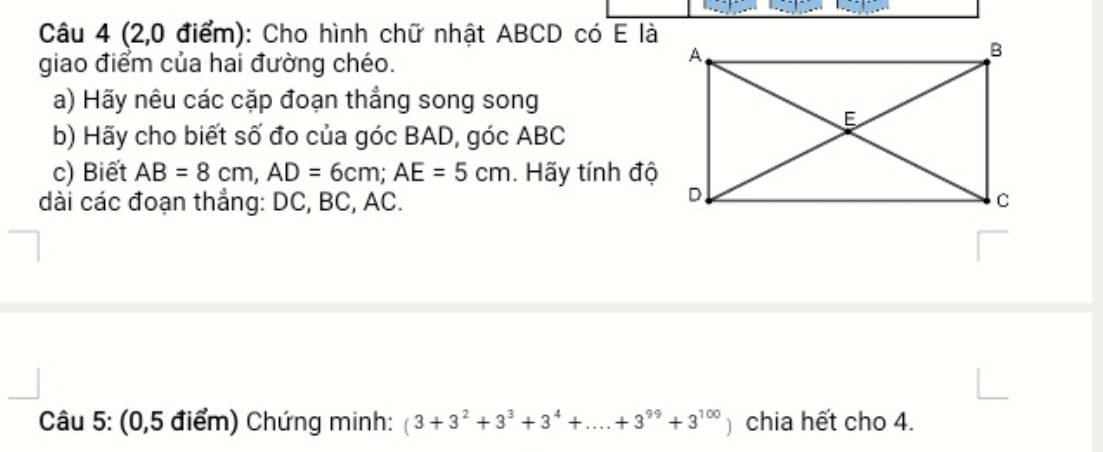
\(\left(3+3^2+3^3+3^4+...+3^{99}+3^{100}\right)\\ =3.\left(1+3\right)+3^3\left(1+3\right)+...+3^{99}\left(1+3\right)\\ =3.4+3^3.4+...+3^{99}.4\\ =4.\left(3+3^3+...+3^{99}\right)⋮4\left(ĐPCM\right)\)

Chiều rộng của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) : \(\dfrac{7}{3}\) = \(\dfrac{9}{4}\) (m)
Chu vi của mảnh vườn hìn chữ nhật là:
(\(\dfrac{21}{4}\) + \(\dfrac{9}{4}\)) x 2 = 15 (m)
Diện tích của mảnh vườn hình chữ nhật là:
\(\dfrac{21}{4}\) x \(\dfrac{9}{4}\) = \(\dfrac{189}{16}\) (m2)
b; Số tiền thu được khi trồng hoa để bán trên mảnh đất hình chữ nhật đó là:
80 000 x \(\dfrac{189}{16}\) = 945 000 (đồng)
KL...
Bài 5:
a, Chiều rộng mảnh vườn:
\(\dfrac{21}{4}:\dfrac{7}{3}=\dfrac{9}{4}\left(m\right)\)
Chu vi mảnh đất:
\(2\times\left(\dfrac{21}{4}+\dfrac{9}{4}\right)=15\left(m\right)\)
Diện tích mảnh đất:
\(\dfrac{21}{4}\times\dfrac{9}{4}=\dfrac{189}{16}\left(m^2\right)\)
b, Số tiền thu được khi bán hoa:
\(\dfrac{189}{16}\times80000=945000\left(đồng\right)\)

\(\dfrac{15}{34}+\dfrac{1}{3}+\dfrac{19}{34}-\dfrac{4}{3}+\dfrac{3}{7}=\left(\dfrac{15}{34}+\dfrac{19}{34}\right)+\left(\dfrac{1}{3}-\dfrac{4}{3}\right)+\dfrac{3}{7}=1-1+\dfrac{3}{7}=\dfrac{3}{7}\)
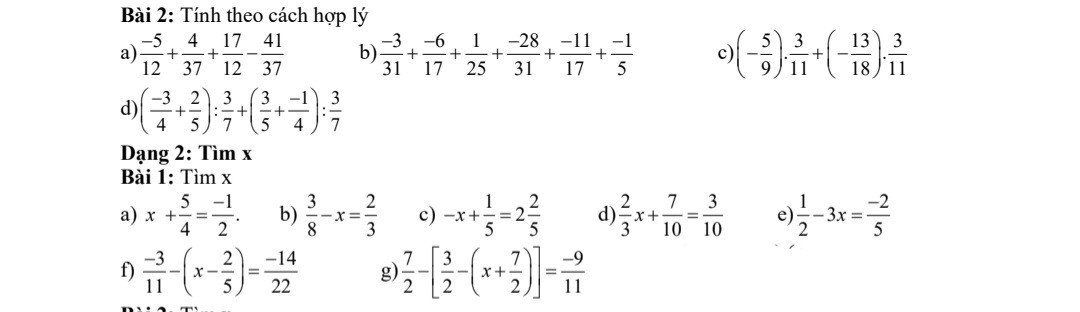
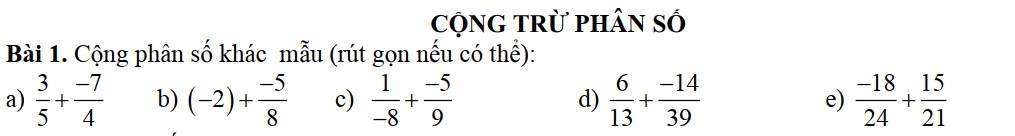

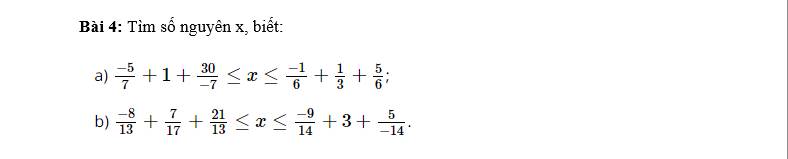


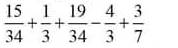
Bài 1:
a: \(x+\dfrac{5}{4}=\dfrac{-1}{2}\)
=>\(x=-\dfrac{1}{2}-\dfrac{5}{4}=-\dfrac{2}{4}-\dfrac{5}{4}=-\dfrac{7}{4}\)
b: \(\dfrac{3}{8}-x=\dfrac{2}{3}\)
=>\(x=\dfrac{3}{8}-\dfrac{2}{3}=\dfrac{9}{24}-\dfrac{16}{24}=-\dfrac{7}{24}\)
c: \(-x+\dfrac{1}{5}=2\dfrac{2}{5}\)
=>\(\dfrac{1}{5}-x=\dfrac{12}{5}\)
=>\(x=\dfrac{1}{5}-\dfrac{12}{5}=-\dfrac{11}{5}\)
d: \(\dfrac{2}{3}x+\dfrac{7}{10}=\dfrac{3}{10}\)
=>\(x\cdot\dfrac{2}{3}=\dfrac{3}{10}-\dfrac{7}{10}=-\dfrac{4}{10}=-\dfrac{2}{5}\)
=>\(x=-\dfrac{2}{5}:\dfrac{2}{3}=-\dfrac{2}{5}\cdot\dfrac{3}{2}=-\dfrac{3}{5}\)
e: \(\dfrac{1}{2}-3x=-\dfrac{2}{5}\)
=>\(3x=\dfrac{1}{2}+\dfrac{2}{5}=\dfrac{5}{10}+\dfrac{4}{10}=\dfrac{9}{10}\)
=>\(x=\dfrac{9}{10}:3=\dfrac{3}{10}\)
f: \(\dfrac{-3}{11}-\left(x-\dfrac{2}{5}\right)=-\dfrac{14}{22}\)
=>\(\dfrac{-3}{11}-\left(x-\dfrac{2}{5}\right)=-\dfrac{7}{11}\)
=>\(x-\dfrac{2}{5}=-\dfrac{3}{11}+\dfrac{7}{11}=\dfrac{4}{11}\)
=>\(x=\dfrac{4}{11}+\dfrac{2}{5}=\dfrac{20}{55}+\dfrac{22}{55}=\dfrac{42}{55}\)
g: \(\dfrac{7}{2}-\left[\dfrac{3}{2}-\left(x+\dfrac{7}{2}\right)\right]=-\dfrac{9}{11}\)
=>\(\dfrac{7}{2}-\dfrac{3}{2}+x+\dfrac{7}{2}=-\dfrac{9}{11}\)
=>\(x+\dfrac{11}{2}=-\dfrac{9}{11}\)
=>\(x=-\dfrac{9}{11}-\dfrac{11}{2}=\dfrac{-18}{22}-\dfrac{121}{22}=\dfrac{-139}{22}\)