Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

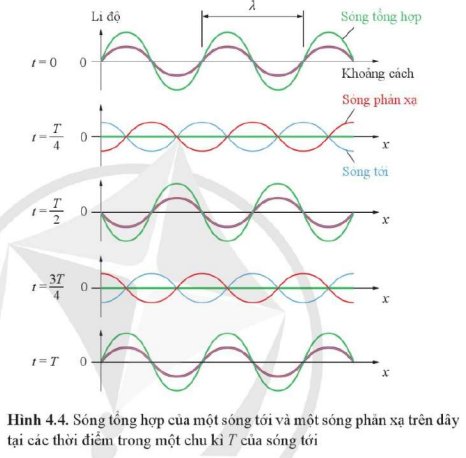
- Bụng sóng là những điểm dao động với biên độ cực đại.
- Biên độ của sóng tổng hợp tại bụng sóng lớn hơn biên độ của sóng tới. Điều đó chứng tỏ tại điểm đó, sóng tới và sóng phản xạ cùng pha, làm tăng cường sóng.

Đáp án C
Khi sóng điện từ lan truyền thì ba vecto E → , B → , v → luôn vuông phương nhau và tạo thành một tam diện thuận.
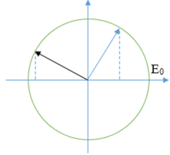
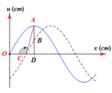
Ở thời điểm t thì cường độ điện trường có giá trị bằng E 0 2 và đang giảm sau đó T/4 thì cường độ điện trường sẽ có giá trị là − E 0 3 2 và đang giảm dần về - E 0 (hình vẽ)
Mà vectơ cường độ điện trường và cảm ứng từ luôn cùng pha, vuông phương nên sau thời gian T/4 thì cảm ứng từ có giá trị bằng − B 0 3 2 .
Xét hướng của cảm ứng từ:
Ở thời điểm t, vecto cường độ điện trường có chiều từ Đông sang Tây, vận tốc truyền sóng có chiều từ Bắc → Nam. Sử dụng quy tắc bàn tay phải “đặt bàn tay phải sao cho chiều từ cổ tay đến các ngón tay chỉ chiều của vecto cường độ điện trường, ngón tay cái choãi ra 900 chỉ chiều của vận tốc truyền sóng thì cảm ứng từ có hướng đi vào lòng bàn tay”. Vậy tại thời điểm t thì vecto cảm ứng từ có hướng từ trên xuống => Sau T/4 thì cảm ứng từ đổi dấu so với ban đầu => vecto cảm ứng từ đổi hướng => có hướng từ dưới lên.

Ta có: \(u=Acos\left(\dfrac{2\pi}{T}t+\dfrac{2\pi x}{\lambda}\right)\)
a, Có: \(\dfrac{2\pi}{T}=2\pi\Rightarrow T=1s\Rightarrow f=\dfrac{1}{T}=1\left(Hz\right)\)
Biên độ A = 10cm
b, Bước sóng: \(\dfrac{2\pi}{\lambda}=0,01\pi\Rightarrow\lambda=200cm\)
Tốc độ truyền sóng: \(v=\lambda f=200\cdot1=200\left(cm/s\right)\)
c, Ta có: \(u=10cos\left(2\pi\cdot4+0,01\pi\cdot50\right)=8,933cm\)

a) Hai nguồn dao động cùng pha thì những điểm nằm trên đường trung trực của đoạn thẳng nối hai nguồn sẽ dao động với biên độ cực đại d2–d1=kλ
b) Hai nguồn dao động ngược pha những điểm nằm trên đường trung trực của đoạn thẳng nối hai nguồn sẽ dao động với biên độ cực tiểu d2–d1=(k+\(\frac{1}{2}\))λ
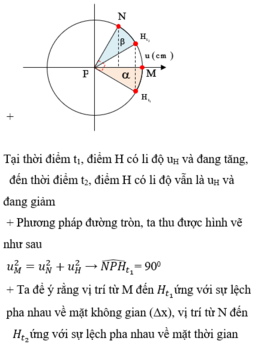
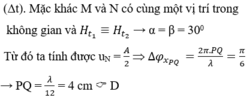




Cường độ sóng I tỉ lệ với bình phương của biên độ sóng A.
\(I = k{A^2}\)(với k là hằng số).
Tại vị trí mà biên độ sóng giảm còn một nửa, cường độ sóng là \(I' = k{\left( {\frac{A}{2}} \right)^2} = \frac{1}{4}k{A^2} = \frac{I}{4}\).
Vậy cường độ sóng giảm đi 4 lần tại vị trí mà biên độ sóng giảm còn một nửa.