Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương pháp giải
Sử dụng: Trong tam giác vuông, cạnh góc vuông bằng cạnh góc vuông kia nhân tan góc đối.

Đặt tên như hình vẽ thì chiều cao của tháp là đoạn BDBD
Xét tam giác ABCABC vuông tại AA có AC=DE=150m;ˆC=200AC=DE=150m;C^=200 nên
AB=150.tan20∘≈54,596(m)AB=150.tan20∘≈54,596(m)
Chiều cao của cột ăng-ten là:
BD=AB+ADBD=AB+AD=54,596+1,5=56,096(m).

Vĩ độ của Hà Nội là 20o01’ có nghĩa là cung kinh tuyến từ Hà Nội đến xích đạo có số đo là . Vậy độ dài cung kinh tuyến từ Hà Nội đến xích đạo là:
l = ≈ 2224 (km)
Vĩ độ của Hà Nội là 20o01’ có nghĩa là cung kinh tuyến từ Hà Nội đến xích đạo có số đo là . Vậy độ dài cung kinh tuyến từ Hà Nội đến xích đạo là:
l = ≈ 2224 (km)

lAB=8050,96(km)
=>3,14*R*72/180=8050,96
=>R=6410(m)
=>OA=6410(m)
AC=6410-6400=10(m)

a) M,N thuộc đường tròn đường kính BC=> Tam giác BMC và tam giác BNC vuông tại M,N
Mà \(\widehat{MAN}=45\Rightarrow\)Tam giác MAC và tam giác NAB vuông cân tại M,N
Khi đó: \(\hept{\begin{cases}OA=OC\\MA=MC\end{cases}\Rightarrow}\)OM là đường trung trực của AC \(\Rightarrow OM\perp AC\)
\(\hept{\begin{cases}OA=OB\\NA=NB\end{cases}\Rightarrow}\)ON là đường trung trực của AB \(\Rightarrow ON\perp AB\)
Vậy O là trực tâm tam giác ABC.
b) \(B,C\in\left(O,OA\right)\Rightarrow OB=OC\)
O thuộc đường tròn đường kính BC=> Tam giác OBC vuông cân tại O \(\Rightarrow\widehat{OBC}=45\)
Tam giác NBA vuông cân tại N \(\Rightarrow\widehat{NBA}=45\)
Vì \(\widehat{OBC}=\widehat{NBA}\) là các góc tại B chắn các cung nhỏ OC và MN của đường tròn đường kính BC \(\Rightarrow MN=OC=BCcos45=\frac{BC}{\sqrt{2}}\)
c) \(\frac{S_{AMN}}{S_{ABC}}=\frac{\frac{1}{2}AM.AN.sin\widehat{MAN}}{\frac{1}{2}AB.AC.sin\widehat{BAC}}=\left(\frac{AM}{AC}\right)\left(\frac{AN}{AB}\right)=cos\widehat{MAN}.cos\widehat{BAC}=cos^245=\frac{1}{2}\)

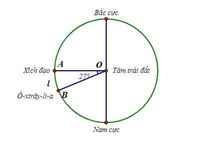

a) Khoảng cách giữa 2 vị trí đó là :
\(\frac{20000}{180}.\left(72-42\right)\simeq2800\left(km\right)\)
b) Bán kính của Trái Đất là :
\(\frac{20000}{3,14}\simeq6400\left(km\right)\)
Độ dài đường xích đạo là :
\(20000.2=40000\left(km\right)\)
Vì trái đất là hình cầu :
Thể tích hình cầu được tính dưới dạng : \(V=\frac{4}{3}.3,14.R^3\)( R là bán kính )
Vậy thể tích Trái Đất là :
\(\frac{4}{3}.3,14.\left(6400\right)^3\simeq1097509547000\left(km^3\right)\)