
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: \(\Leftrightarrow2\cdot\cos2x\cdot\cos x+2\cdot\sin x\cdot\cos2x=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow2\cdot\cos2x\left(\sin x+\cos x\right)=\sqrt{2}\cdot\cos2x\)
\(\Leftrightarrow\sqrt{2}\cdot\cos2x\cdot\left[\sqrt{2}\cdot\sqrt{2}\cdot\sin\left(x+\dfrac{\Pi}{4}\right)-1\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\cos2x=0\\\sin\left(x+\dfrac{\Pi}{4}\right)=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{\Pi}{2}+k\Pi\\x+\dfrac{\Pi}{4}=\dfrac{\Pi}{6}+k2\Pi\\x+\dfrac{\Pi}{4}=\dfrac{5}{6}\Pi+k2\Pi\end{matrix}\right.\)
\(\Leftrightarrow x\in\left\{\dfrac{\Pi}{4}+\dfrac{k\Pi}{2};\dfrac{-1}{12}\Pi+k2\Pi;\dfrac{7}{12}\Pi+k2\Pi\right\}\)
c: \(\Leftrightarrow2\cdot\sin2x\cdot\cos x+\sin2x=2\cdot\cos2x\cdot\cos x+\cos2x\)
\(\Leftrightarrow\sin2x\left(2\cos x+1\right)=\cos2x\left(2\cos x+1\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}\sin2x=\cos2x=\sin\left(\dfrac{\Pi}{2}-2x\right)\\\cos x=-\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\Pi}{8}+\dfrac{k\Pi}{4}\\\\x=-\dfrac{2}{3}\Pi+k2\Pi\\x=\dfrac{2}{3}\Pi+k2\Pi\end{matrix}\right.\)

Chọn D
Ta sẽ biến đổi phương trình thành dạng tích
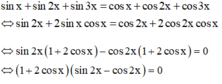
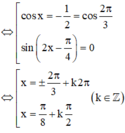
Chú ý: có thể dùng 4 đáp án thay vào phương trình để kiểm tra đâu là nghiệm

a.\(\frac{k\Pi}{2}+\frac{\alpha}{2}\)
b.\(\left\{{}\begin{matrix}x=\frac{1}{4}arcsin\left(\frac{1}{3}\right)+\frac{k\Pi}{2}-\frac{1}{8}\\x=\Pi-\frac{1}{4}arcsin\left(\frac{1}{3}\right)+\frac{k\Pi}{2}-\frac{1}{8}\end{matrix}\right.\)

a.
\(\Leftrightarrow\frac{2}{\sqrt{5}}sinx-\frac{1}{\sqrt{5}}cosx=\frac{2}{\sqrt{5}}\)
Đặt \(\frac{2}{\sqrt{5}}=cosa\) với \(a\in\left(0;\pi\right)\)
\(\Rightarrow sinx.cosa-cosx.sina=cosa\)
\(\Leftrightarrow sin\left(x-a\right)=sin\left(\frac{\pi}{2}-a\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}x-a=\frac{\pi}{2}-a+k2\pi\\x-a=\frac{\pi}{2}+a+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\frac{\pi}{2}+k2\pi\\x=\frac{\pi}{2}+2a+k2\pi\end{matrix}\right.\)
b.
\(\Leftrightarrow\sqrt{2}sin\left(3x+\frac{\pi}{4}\right)=1\)
\(\Leftrightarrow sin\left(3x+\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+\frac{\pi}{4}=\frac{\pi}{4}+k2\pi\\3x+\frac{\pi}{4}=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
c.
\(\Leftrightarrow\frac{1}{2}sin2x-\frac{\sqrt{3}}{2}cos2x=\frac{1}{2}\)
\(\Leftrightarrow sin\left(2x-\frac{\pi}{3}\right)=\frac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-\frac{\pi}{3}=\frac{\pi}{6}+k2\pi\\2x-\frac{\pi}{3}=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow...\)
Câu cuối là \(-cosx\) hay \(-cos2x\) bạn?


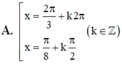
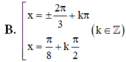




\(pt\Leftrightarrow\left(cosx+sinx\right)\left(sin^2x+cos^2x-sinx.cosx\right)=cosx+sinx+sin2x\)
\(\Leftrightarrow\left(cosx+sinx\right)\left(1-sinx.cosx-1\right)=sin2x\)
\(\Leftrightarrow-\dfrac{1}{2}sin2x\left(cosx+sinx\right)=sin2x\)
\(\Leftrightarrow sin2x\left(cosx+sinx+2\right)=0\)
\(\Leftrightarrow sin2x\left[\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\right]=0\)
\(\Leftrightarrow sin2x=0\)
\(\Leftrightarrow x=\dfrac{k\pi}{2}\)