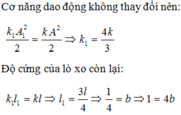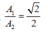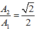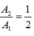Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khi giữ tại điểm đó thì chiều dài của lò xo chỉ còn 3/4 chiều dài ban đầu, do đó độ cứng k sẽ tăng lên bằng 4/3 độ cứng ban đầu.
Tần số dao động sẽ tăng lên \(2\sqrt{3}\) lần
Ở vị trí cân bằng vận tốc của vật cực đại và không đổi khi giữ điểm đó
\(A'=\frac{v}{\omega'}=\frac{A\omega}{\omega'}=\frac{A\sqrt{3}}{2}\)
\(\rightarrow B\)

Tại thời điểm giữ lò xo thì: \(W_{d}=W_{t}=\dfrac{W}{2}\)
Cố định 1 điểm chính giữa lò xo thì thế năng giảm đi 1 nửa
\(\Rightarrow W_{t'}=\dfrac{W_t}{2}=\dfrac{W}{4};W_{đ}=\dfrac{W}{2}\Rightarrow W'=\dfrac{3W}{4}\)
Có: \(k'=2k\Rightarrow \dfrac{3}{4}.kA^{2}=k'A'^{2}\)
\(\Rightarrow \dfrac{A}{A'}=\dfrac{4}{\sqrt{6}}\)

Đáp án B
Phương pháp: Định luật bảo toàn cơ năng
Cách giải:
+ Đúng lúc vật đi qua VTCB, người ta giữ cố định điểm chính giữa của lò xo => l2 = l1/2
+ Độ cứng tỉ lệ nghịch với chiều dài tự nhiên của nó => k2 = 2k1
có 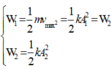
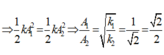

Khi lò xo bị giữ lại tại điểm chính giữa, nghĩa là chiều dài của lò xo chỉ còn một nửa như vậy độ cứng của lò xo tăng thêm 2 lần
Suy ra tần số góc của dao động mới \(\omega_2=\sqrt{\frac{2k}{m}}\) tăng lên \(\sqrt{2}\) so với tần số dao động cũ.
Khi qua vị trí cân bằng thì vận tốc cực đại được tình theo công thức
\(v_{max}=A\omega\)
Trong bài này vận tốc cực đại không đổi
\(A_2=\frac{A}{\sqrt{2}}\)