Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình chẳng thấy đáp án nào đúng cả. Bạn xem lại xem có sai gì không nhé.

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

Khi vật I qua VTCB thì nó có vận tốc là: \(v=\omega.A\)
Khi thả nhẹ vật II lên trên vật I thì động lượng được bảo toàn
\(\Rightarrow M.v = (M+m)v'\Rightarrow v'=\dfrac{3}{4}v\)
Mà \(v'=\omega'.A'\)
\(\dfrac{v'}{v}=\dfrac{\omega'}{\omega}.\dfrac{A'}{A}=\sqrt{\dfrac{M}{\dfrac{4}{3}M}}.\dfrac{A'}{A}=\dfrac{3}{4}\)
\(\Rightarrow \dfrac{A'}{A}=\dfrac{\sqrt 3}{2}\)
\(\Rightarrow A'=5\sqrt 3cm\)
Chọn A.
Vận tốc của M khi qua VTCB: v = ωA = 10.5 = 50cm/s
Vận tốc của hai vật sau khi m dính vào M: v’ = Mv/(M+v)= 40cm/s
Cơ năng của hệ khi m dính vào M: W = 1/2KA'2= 1/2(m+M)v'2
A’ = 2căn5

Chọn đáp án A
? Lời giải:

+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng

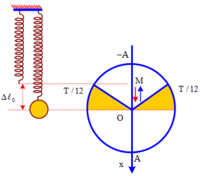
+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
![]()

Chọn đáp án A
? Lời giải:
+ Lực đàn hồi đổi chiều tại vị trí lò xo không biến dạng.
+ Lực hồi phục (kéo về) đổi chiều tại vị trí cân bằng
f = 1 2 π g Δ l ⇒ Δ l = 1 c m A = Δ l 2 + v 2 ω 2 = 2 c m ⇒ Δ l = A 2
+ Thời gian mà lực đàn hồi ngược chiều lực hồi phục khi vật đi từ O đến M (M là vị trí lò xo không biến dạng) và ngược lại
Δ t = 2. T 12 = T 6 = 1 30 s

\(\omega=2\pi f = 9\pi (rad/s)\)
Biên độ \(A=(56-40)/2=8(cm)\)
Gốc thời gian lúc lò xo ngắn nhất --> biên độ (-A) -->\(\varphi=-\pi (rad)\)
Vậy: \(x=8\cos(9\pi t-\pi)(cm)\)
Chọn D.

Tần số góc: \(\omega=\sqrt{\frac{K}{m}}=10\pi\left(rad\text{/}s\right)\)
Biên độ dao động của vật \(A=\sqrt{x^2+\left(\frac{v}{w}\right)^2}=6\left(cm\right)\)
Lò xo có độ nén cực đại tại biên âm:
\(\Rightarrow\) Góc quét \(=\pi\text{/}3+\pi=\omega t\Rightarrow t=2\text{/}15\left(s\right)\)
chọn B
Đáp án C