Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
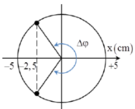
+ Độ biến dạng của lò xo tại vị trí cân bằng:
![]()
+ Lực đàn hồi tác dụng lên vật thỏa mãn:
|Fđh| > 1,5N khi |Δl| > 0,015m = 1,5cm hay -2,5 cm < x < 5cm.
+ Từ hình vẽ ta xác định được khoảng thời gian tương ứng là:
![]()

Ta có: \(F=-k.x\)
\(\Rightarrow x = -\dfrac{F}{k}=-0,05\cos(2\pi t-\dfrac{5\pi}{6})(m)\)
Vận tốc: \(v=v'_{(t)}=0,1.\pi.\sin(2\pi t-\dfrac{5\pi}{6})\)(m/s)
Đến đây chưa xong nha
Bạn phải biến đổi tiếp từ x = -0,05.cos(2πt - \(\dfrac{5\pi}{6}\)) = 0,05.cos(2πt - \(\dfrac{\pi}{6}\))(m)
=> x = 5.cos(2πt - \(\dfrac{\pi}{6}\)) (cm)
=> v = 10π.sin(2πt - \(\dfrac{\pi}{6}\)) = 10π.cos(2πt + \(\dfrac{2\pi}{3}\)) < Đây mới là đáp án cuối cùng nha>

Chọn C
W= 1 2 m . w 2 A 2 = 1 2 0 , 2 . 20 2 . ( 5 . 10 - 2 ) 2 = 0 , 1 J

Đáp án D
Phương pháp: Sử dụng lí thuyết về lực đàn hồi trong dao động điều hòa của CLLX ngang và đường tròn lượng giác
Cách giải:
+ Đối với CLLX ngang thì lực đàn hồi đổi chiều tại VTCB
+ Biểu diễn trên đường tròn lượng giác :
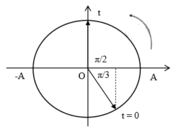
Góc quét được:
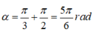
=> Từ t = 0 thì vật đi qua VTCB lần đầu tại thời điểm:
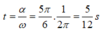

\(l_{max}=l_0+\Delta l+A\Rightarrow\left\{{}\begin{matrix}A=5cm=0,02m\\\Delta l=\dfrac{g}{\omega^2}=\dfrac{10}{\left(10\right)^2}=0,1m\\l_0=0,2m\end{matrix}\right.\)
=> \(l_{max}=0,2+0,1+0,02=0,32\left(m\right)=32cm\)
\(l_{min}=l_0+\Delta l-A=0,2+0,1-0,02=0,28\left(m\right)=28\left(cm\right)\)
Vậy ...

\(A=2cm,\Delta l=10cm,l_0=50cm.\)
Lực đàn hồi cực đại của con lắc lò xo treo thẳng đứng \(F_{dhmax}=k\left(A+\Delta l\right).\)
Lực kéo về tại vị trí có li độ \(x\) là \(F=kx\)
=> \(\frac{A+\Delta l}{x}=12\Rightarrow x=\frac{2+10}{12}=1cm.\)
khi vật ở li độ x = 1cm thì lò xo dãn là \(\Delta l+x=11cm.\)
