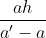Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 
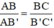(hệ quả định lý Talet)
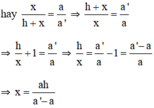
Ta có:
ABAB′ABAB′ = BCBC′BCBC′ mà AB' = x + h nên
xx+hxx+h = aa′aa′ <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x= aha′−aaha′−a
Vậy khoảng cách AB bằng aha′−a
Tham khảo:
5.Dòng nước đã đẩy chiếc đò lệch đi một góc là:
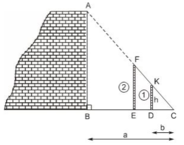
a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A, F, K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
b) ΔABC có AB // KD (D ∈ BC, K ∈ AC)
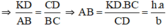
Vậy chiều cao bức tường là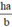 
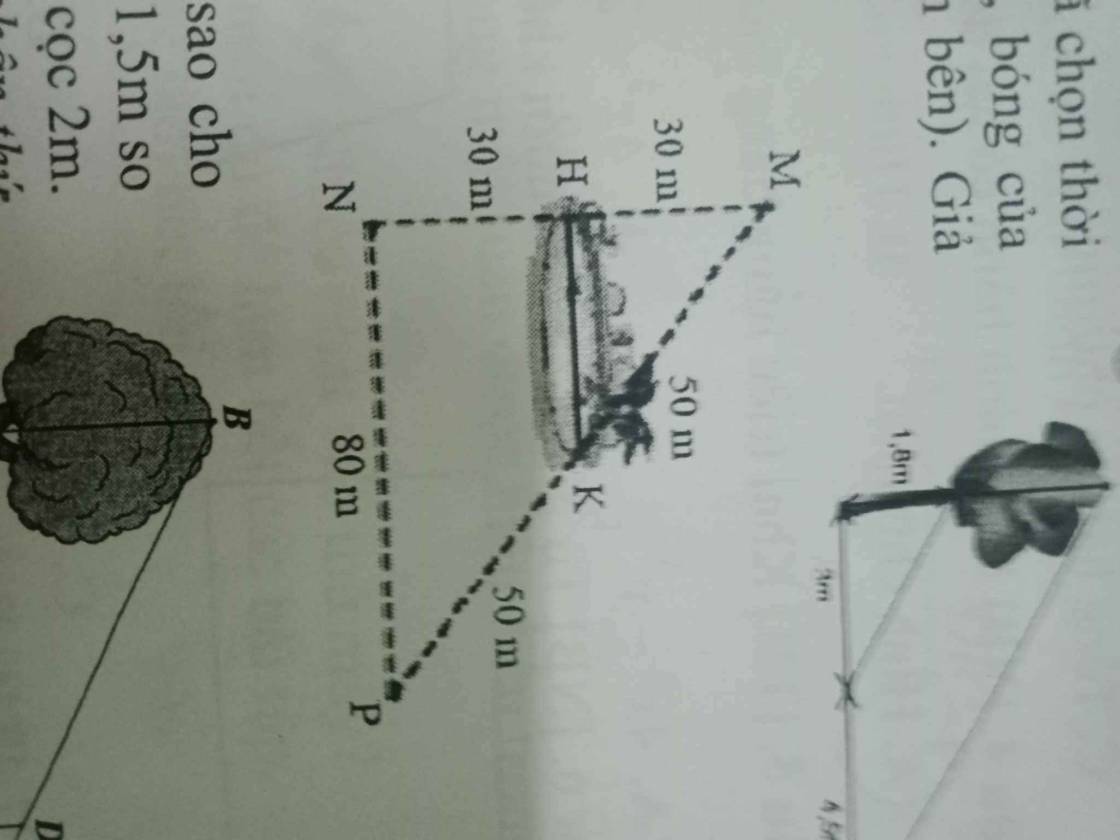
Ta có:
MN = MH + HN = 30 + 30 = 60 (m)
MP = MK + KP = 50 + 50 = 100
Lại có:
MH/MN = 30/60 = 1/2
MK/MP = 50/100 = 1/2
⇒ MH/MN = MK/MP = 1/2
⇒ HK // MN
⇒ HK/NP = MH/MN = 1/2
⇒ HK = NP : 2
= 80 : 2
= 40 (m)
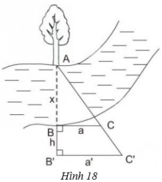
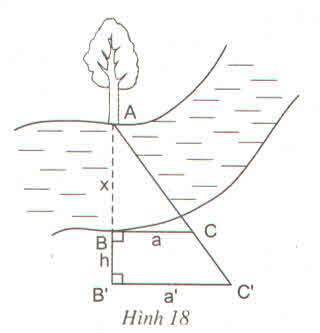
Ta có hình như sau :
giải :
Ta có:
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=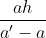
Vậy khoảng cách AB bằng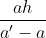
Ta có hình như sau :
Giải
Ta có:
<=> a'x - ax = ah
<=> x(a' - a) = ah
x=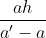
Vậy khoảng cách AB bằng