Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

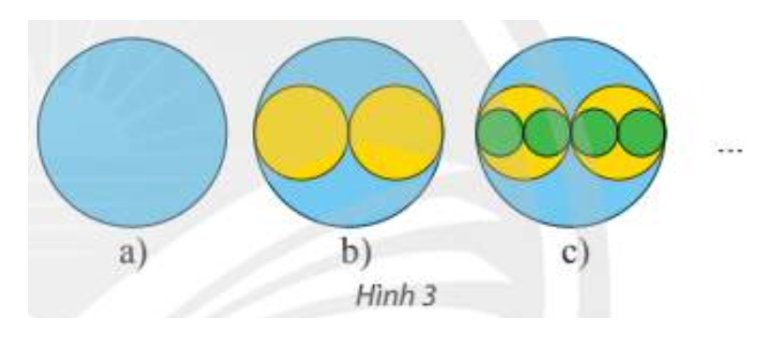
Giả sử các hình tròn bán kính \({R_1} = R,{R_2} = \frac{R}{2},{R_3} = \frac{R}{4} = \frac{R}{{{2^2}}},...,{R_n} = \frac{R}{{{2^{n - 1}}}},...\) có diện tích lần lượt là \({u_1},{u_2},{u_3},...,{u_n},...\) Ta có:
\(\begin{array}{l}{u_1} = \pi R_1^2 = \pi {R^2},{u_2} = \pi R_2^2 = \pi {\left( {\frac{R}{2}} \right)^2} = \pi {R^2}.\frac{1}{{{2^2}}},{u_3} = \pi R_3^2 = \pi {\left( {\frac{R}{{{2^2}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^4}}},...,\\{u_n} = \pi R_n^2 = \pi {\left( {\frac{R}{{{2^{n - 1}}}}} \right)^2} = \pi {R^2}.\frac{1}{{{2^{2n - 2}}}},...\end{array}\)
\(\begin{array}{l}S = {u_1} + {u_2} + ... + {u_n} + ... = \pi {R^2} + 2\pi {R^2}.\frac{1}{{{2^2}}} + 4.\pi {R^2}.\frac{1}{{{2^4}}} + ... + {2^{n + 1}}\pi {R^2}.\frac{1}{{{2^{2n - 2}}}} + ...\\\,\,\,\, = \pi {R^2} + \pi {R^2}.\frac{1}{2} + \pi {R^2}.\frac{1}{{{2^2}}} + ... + \pi {R^2}.\frac{1}{{{2^{n - 1}}}} + ...\\\,\,\,\, = \pi {R^2}\left( {1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...} \right)\end{array}\)
Xét tổng: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ...\)
Tổng trên là tổng của cấp số nhân lùi vô hạn có số hạng đầu \({u_1} = 1\) và công bội \(q = \frac{1}{2}\) nên: \({S_n} = 1 + \frac{1}{2} + \frac{1}{{{2^2}}} + ... + \frac{1}{{{2^{n - 1}}}} + ... = \frac{1}{{1 - \frac{1}{2}}} = 2\).
Vậy \(S = \pi {R^2}.{S_n} = 2\pi {R^2}\).

Mỗi lần cắt một mảnh giấy thành 7 mảnh, tức là Mạnh tạo thêm 6 mảnh giấy. Do đó công thức tính số mảnh giấy theo n bước được thực hiện là Sn = 6n + 1. Ta chứng minh tính đúng đắn của công thức trên bằng phương pháp quy nạp theo n.
Bước cơ sở. Mạnh cắt mảnh giấy thành 7 mảnh, n =1, S(1) = 6.1+1 =7
Công thức đúng với n = 1
Bước quy nạp: giả sử sau k bước, Mạnh nhận được số mảnh giấy là S(k) = 6k + 1
Sang bước thứ k +1, Mạnh lấy một trong số những mảnh giấy nhận được trong k bước trước và cắt thành 7 mảnh. Tức là Mạnh đã lấy đi 1 trong S(k) mảnh và thay vào đó 7 mảnh được cắt ra. Vậy tổng số mảnh giấy ở bước k + 1 là: S(k =1) = S(k) -1 + 7= S(k) + 6 = 6k + 1 + 1 = 6(k+1) +1
Vậy công thức S(n) đúng với mọi n ∈N* . Theo công thức trên chỉ có phương án D thoả mãn vì 121 =6.20 + 1
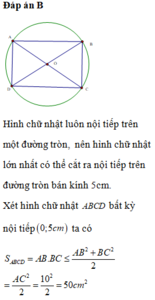
Đáp án D

a) Ta có:
\(\begin{array}{l}{u_1} = 25\\{u_2} = 24 = {u_1} - 1\\{u_3} = 23 = {u_2} - 1\\ \vdots \end{array}\)
Vậy công thức truy hồi: \({u_n} = {u_{n - 1}} - 1\left( {n \ge 2} \right) \Leftrightarrow {u_n} - {u_{n - 1}} = - 1 < 0\).
Vậy \(\left( {{u_n}} \right)\) là dãy số giảm.
b) Ta có:
\(\begin{array}{l}{v_1} = 14\\{v_2} = 15 = {v_1} + 1\\{v_3} = 16 = {v_2} + 1\\ \vdots \end{array}\)
Vậy công thức truy hồi: \({v_n} = {v_{n - 1}} + 1\left( {n \ge 2} \right) \Leftrightarrow {v_n} - {v_{n - 1}} = 1 > 0\).
Vậy \(\left( {{v_n}} \right)\) là dãy số tăng.

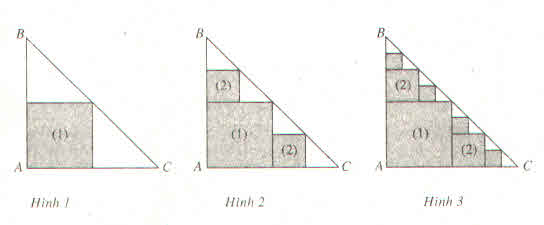
a) Hình vuông thứ nhất có cạnh bằng nên u1 = (
)2 =
.
Hình vuông thứ hai có cạnh bằng nên u2 = (
)2 =
.
Hình vuông thứ ba có cạnh bằng nên u3 = (
)2 =
.
Tương tự, ta có un =
b) Dãy số (un) là một cặp số nhân lùi vô hạn với u1 = và q =
. Do đó
lim Sn = .




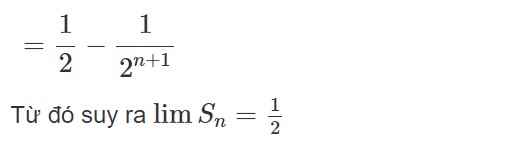

a) giá trị của un rất lớn khi n tăng lên vô hạn
b) Cần n > 384.1010 tờ giấy để đạt được những chồng giấy có về dày lớn hơn khoảng cách từ Trái Đất tới Mặt Trăng