NT
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
ND
1
23 tháng 7 2017
Chu vi của tam giác abc là
ab+bc+c=25 (1)
chu vi của tam giác acd là (2)
ac+cd+da=17 (3)
chu vi của tứ giác abcd là
ab+bc+cd+da=32
từ (1) và (2) ta có :
ab+bc+ac+ac+cd+da=25+27=52
=>(ab=bc=cd=da)+2ac=52 (4)
từ (1) và (4)
<=> 32+2ac=52
=>2ac =52 - 32 =20
=>ac=20:2=10
vậy ac = 10cm
18 tháng 10 2023
Gọi độ dài hai cạnh góc vuông lần lượt là a(m),b(m)(ĐK: a>0;b>0)
Độ dài hai cạnh góc vuông tỉ lệ với 3 và 4 nên \(\dfrac{a}{3}=\dfrac{b}{4}=k\)
=>a=3k; b=4k
Theo đề, ta có: \(a^2+b^2=20^2\)
=>\(25k^2=400\)
=>\(k^2=16\)
=>k=4
=>a=3*4=12; b=4*4=16
20 tháng 10 2023
a: Đặt \(\dfrac{AB}{5}=\dfrac{AC}{12}=k\)
=>AB=5k; AC=12k
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(25k^2+144k^2=26^2\)
=>\(k^2=4\)
=>k=2
=>AB=10cm; AC=24cm
b: Xét tứ giác ABCD có
\(\widehat{A}+\widehat{B}+\widehat{BCD}+\widehat{ADC}=360^0\)
=>\(\widehat{BCD}+\widehat{ADC}=360^0-70^0=290^0\)
=>\(2\cdot\left(\widehat{ODC}+\widehat{OCD}\right)=290^0\)
=>\(\widehat{OCD}+\widehat{ODC}=145^0\)
Xét ΔOCD có \(\widehat{COD}+\widehat{OCD}+\widehat{ODC}=180^0\)
=>\(\widehat{COD}=180^0-145^0=35^0\)
13 tháng 2 2016
Gọi 3 đường cao là a,b,c còn 3 cạnh là x,y,z
Ta có x/2=y/3=z/4 (giả thiết) và x.a=y.b=z.c (1) (dựa vào công thức tính diện tích tam giác)
x/2=y/3=z/4=k thì x=2k, y=3k, z=4k thay vào (1) ta được:
2k.a=3k.b=4k.c suy ra a/6=b/4=c/3 (chia cho 12k)
Vậy 3 đường cao tương ứng tỉ lệ 6,3,4
4 tháng 3 2021
Gọi độ dài ba cạnh của tam giác đó lần lượt là x,y,z.Theo đề bài ta có :
x : y : z = 3 : 4 : 5 hay \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{60}{12}=5\)
=> x= 5.3 = 15,y = 5.4 = 20,z = 5.5 = 25
Vậy độ dài của ba cạnh lần lượt là 15cm,20cm,25cm
LM
Lê Minh Vũ
CTVHS
18 tháng 11 2021
Gọi độ dài 3 cạnh của tam giác lần lượt là \(a,b,c\inℕ^∗;a,b,c\left(cm\right)\)
Do độ dài 3 cạnh tỉ lệ với \(3,4,5\)
\(\Rightarrow\)\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Do chu vi của tam giác là \(60cm\)
\(\Rightarrow\)\(a+b+c=60\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)
Do đó:
\(\frac{a}{3}=5\Rightarrow a=5.3=15\)
\(\frac{b}{4}=5\Rightarrow b=5.4=20\)
\(\frac{c}{5}=5\Rightarrow c=5.5=25\)
Vậy độ dài lần lượt của 3 cạnh tam giác lần lượt là: \(15,20,25\)
CM
18 tháng 6 2018
Vì 
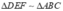nên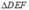 
cũng có độ dài các cạnh tỉ lệ với 4 : 5 : 6.
Giả sử DE < EF < FD Þ DE = 0,8m.
Ta có
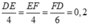
Từ đó tính được EF = 1m và FD = 1,2m