


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án D
Ta có z . z ¯ = z 2 ⇒ z . z ¯ + z = 2 ⇔ z 2 + z = 2 ⇔ z + 4 = 2 (do z = 2 )
Đặt z = x + y i , x ; y ∈ ℝ
Ta có
z + 4 = 2 z = 2 ⇔ x + 4 2 + y 2 = 4 x 2 + y 2 = 2 ⇔ x + 4 − x x + 4 + x = 0 x 2 + y 2 = 4 ⇔ x = − 2 y = 0
Vậy có duy nhất một giá trị z = − 2 thảo mãn yêu cầu đề bài

Đặt z=a+bi ta có z = 2 ⇔ a 2 + b 2 = 4 ( 1 )
Và ![]()
![]()
Biểu diễn (1), (2) trên cùng hệ trục toạ độ:
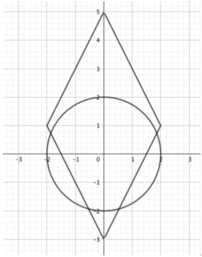
Chúng cắt nhau tại 4 điểm phân biệt, tức có 4 số phức thoả mãn.
Chọn đáp án C.
*Chú ý cách giải trên là nhanh nhất, các em có thể xét các trường hợp của trị tuyệt đối và giải hệ phương trình.
*Hình thoi trên hình vẽ được vẽ nhanh bằng cách đi tìm các đỉnh của nó, đó là giải các hệ phương trình
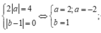
![]()
Chọn đáp án C.

Đáp án D.
Đặt z = x + y i , x , y ∈ ℝ ⇒ z = 2 ⇔ x 2 + y 2 = 2 ( 1 )
z 2 = x 2 − y 2 + 2 x y i là số thuần ảo ⇔ x 2 − y 2 = 0 ( 2 ) x y ≠ 0
Từ (1) và (2) ta có hệ x 2 + y 2 = 2 x 2 − y 2 = 0 (ĐK: x y ≠ 0 )
⇔ 2 x 2 = 2 x 2 − y 2 = 0 ⇔ x = 1 x = − 1 y 2 = 1 ⇒ x = 1 y = 1 x = 1 y = − 1 x = − 1 y = 1 x = − 1 y = − 1
Có 4 số phức z thỏa mãn.