Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tham khảo:
Có bao nhiêu nghiệm nguyên m để hàm số f(x)= m(2020 x-2cosx) sinx -x nghịch biến trên R A .vô số B.2 C.1 D.0 - Hoc24

\(f'\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x-sinx=0\\x-m-3=0\\x-\sqrt{9-m^2}=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=m+3\\x=\sqrt{9-m^2}\end{matrix}\right.\)
Do hệ số bậc cao nhất của x dương nên:
- Nếu \(m=-3\Rightarrow f'\left(x\right)=0\) có nghiệm bội 3 \(x=0\) \(\Rightarrow x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m=3\Rightarrow x=0\) là nghiệm bội chẵn (không phải cực trị, ktm)
- Nếu \(m=0\Rightarrow x=3\) là nghiệm bội chẵn và \(x=0\) là nghiệm bội lẻ, đồng thời \(x=0\) là cực tiểu (thỏa mãn)
- Nếu \(m\ne0;\pm3\) , từ ĐKXĐ của m \(\Rightarrow-3< m< 3\Rightarrow\left\{{}\begin{matrix}m+3>0\\\sqrt{9-m^2}>0\end{matrix}\right.\)
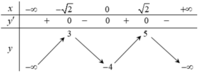
Khi đó \(f'\left(x\right)=0\) có 3 nghiệm pb trong đó \(x=0\) là nghiệm nhỏ nhất
Từ BBT ta thấy \(x=0\) là cực tiểu
Vậy \(-3\le m< 3\)
cho em hỏi là tại sao m≠0 mà đkxđ của m lại là -3<m<3 ạ ?

Theo mình:
để hàm số đồng biến, đk cần là y'=0.
a>0 và \(\Delta'< 0\)
nghịch biến thì a<0
vì denta<0 thì hầm số cùng dấu với a
mình giải được câu a với b
câu c có hai cực trị thì a\(\ne\)0, y'=0, denta>0 (để hàm số có hai nghiệm pb)
câu d dùng viet
câu e mình chưa chắc lắm ^^

Chọn đáp án A.
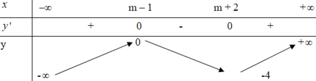
Hàm số đã cho nghịch biến trên khoảng m - 1 ; m + 2
Vậy để hàm số f x nghịch biến trên khoảng 2 ; 3
![]()
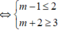
![]()





\(f'\left(x\right)=m\left(1+2sinx\right)+cosx-1\)
\(f'\left(x\right)=2m.sinx+cosx+m-1\)
\(f'\left(x\right)\le\sqrt{\left(4m^2+1\right)\left(sin^2x+cos^2x\right)}+m-1=\sqrt{4m^2+1}+m-1\)
Để hàm số nghịch biến trên R
\(\Leftrightarrow f'\left(x\right)\le0;\forall x\)
\(\Rightarrow\sqrt{4m^2+1}+m-1\le0\)
\(\Leftrightarrow\sqrt{4m^2+1}\le1-m\) (\(m\le1\))
\(\Rightarrow4m^2+1\le1-2m+m^2\)
\(\Rightarrow3m^2+2m\le0\Rightarrow-\frac{2}{3}\le m\le0\)
Có đúng 1 giá trị nguyên của m là \(m=0\) thỏa mãn