K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
20 tháng 11 2019
Chọn B
Nếu m = 1 thì y = 1 (không thỏa mãn tổng của giá trị lớn nhất và nhỏ nhất bằng 8)
Nếu m
≠
1 thì hàm số đã cho liên tục trên [1;2] và 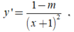
Khi đó đạo hàm của hàm số không đổi dấu trên đoạn [1;2]
Do vậy ![]()

24 tháng 3 2016
- Khi \(m=0\Rightarrow y=x-1\) nên hàm số không có cực trị
- Khi \(m\ne0\Rightarrow y'=3mx^2+6mx-\left(m-1\right)\)
hàm số không có cực trị khi và chỉ chỉ y' = 0 không có nghiệm hoặc có nghiệm kép
\(\Leftrightarrow\Delta'=9m^2+3m\left(m-1\right)=12m^2-3m\le0\) \(\Leftrightarrow0\le m\)\(\le\frac{1}{4}\)

