Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Rõ ràng nếu
m
2
-
m
≠
0
⇔ 
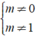thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.
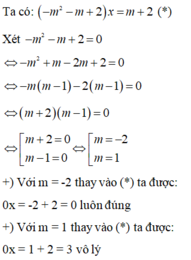
Vậy với m = -2 thì phương trình đã cho có vô số nghiệm.
Đáp án cần chọn là: C
\(\left\{{}\begin{matrix}m\left(x+3\right)\le x+5\\m\left(x+2\right)\ge x+3\end{matrix}\right.\) có nghiệm chung \(\left(1\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{x+5}{x+3}\\m\ge\dfrac{x+3}{x+2}\end{matrix}\right.\)
Để 2 pt có 1 nghệm chung thì \(\dfrac{x+5}{x+3}=\dfrac{x+3}{x+2}\)
\(\Leftrightarrow\left(x+5\right)\left(x+2\right)-\left(x+3\right)^2=0\)
\(\Leftrightarrow x^2+7x+10-x^2-6x-9=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Thay \(x=-1\) vào \(\left(1\right):\)
\(\left\{{}\begin{matrix}m\left(-1+3\right)\le-1+5\\m\left(-1+2\right)\ge-1+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m\le4\\m\ge2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le2\\m\ge2\end{matrix}\right.\)
\(\Rightarrow m=2\)
Vậy m = 2 thì bpt trên có nghiệm chung
Ta có: m(x - 1) < 3 – x
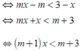
Bất phương trình tương đương là ( m + 1 )x < m + 3
Rõ ràng với m ≠ - 1 thì bất phương trình luôn có nghiệm
Với m = - 1 ta có bất phương trình có dạng: 0x < 2 luôn đúng với mọi x
Vậy bất phương trình có nghiệm với mọi m.
Chọn đáp án C.
Rõ ràng: m 2 + m - 6 ≠ 0 thì bất phương trình luôn có nghiệm
Xét m 2 + m - 6 = 0
Từ hai trường hợp, ta được bất phương trình có nghiệm khi m ≠ 2
Chọn đáp án A.
Rõ ràng nếu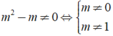
thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.