Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Rõ ràng nếu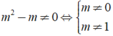
thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.
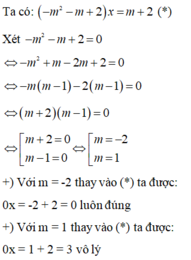
Vậy với m = -2 thì phương trình đã cho có vô số nghiệm.
Đáp án cần chọn là: C
\(\left\{{}\begin{matrix}m\left(x+3\right)\le x+5\\m\left(x+2\right)\ge x+3\end{matrix}\right.\) có nghiệm chung \(\left(1\right)\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le\dfrac{x+5}{x+3}\\m\ge\dfrac{x+3}{x+2}\end{matrix}\right.\)
Để 2 pt có 1 nghệm chung thì \(\dfrac{x+5}{x+3}=\dfrac{x+3}{x+2}\)
\(\Leftrightarrow\left(x+5\right)\left(x+2\right)-\left(x+3\right)^2=0\)
\(\Leftrightarrow x^2+7x+10-x^2-6x-9=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\)
Thay \(x=-1\) vào \(\left(1\right):\)
\(\left\{{}\begin{matrix}m\left(-1+3\right)\le-1+5\\m\left(-1+2\right)\ge-1+3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2m\le4\\m\ge2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\le2\\m\ge2\end{matrix}\right.\)
\(\Rightarrow m=2\)
Vậy m = 2 thì bpt trên có nghiệm chung
Ta có: m(x - 1) < 3 – x
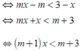
Bất phương trình tương đương là ( m + 1 )x < m + 3
Rõ ràng với m ≠ - 1 thì bất phương trình luôn có nghiệm
Với m = - 1 ta có bất phương trình có dạng: 0x < 2 luôn đúng với mọi x
Vậy bất phương trình có nghiệm với mọi m.
Chọn đáp án C.
Rõ ràng: m 2 + m - 6 ≠ 0 thì bất phương trình luôn có nghiệm
Xét m 2 + m - 6 = 0
Từ hai trường hợp, ta được bất phương trình có nghiệm khi m ≠ 2
Chọn đáp án A.
Rõ ràng nếu m 2 - m ≠ 0 ⇔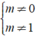
thì bất phương trình luôn có nghiệm.
Với m = 0, bất phương trình trở thành 0x < 0: vô nghiệm.
Với m = 1, bất phương trình trở thành 0x < 1: luôn đúng với mọi x ∈ R
Vậy với m = 0 thì bất phương trình trên vô nghiệm.