Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để tính số mạch điện khác nhau có thể mắc từ 3 điện trở R1, R2, R3, ta sử dụng công thức tính số cách kết hợp chập k của n phần tử. Trong trường hợp này, chúng ta có n = 3 và k = 3.
Số mạch điện khác nhau = C(3, 3) = 1
Vậy có 1 mạch điện khác nhau có thể mắc từ 3 điện trở R1, R2, R3.
Điện trở tương đương của mạch điện này là R1 + R2 + R3 = 10 + 10 + 30 = 50 Ω.
b) Để mắc cả 4 điện trở thành mạch điện có điện trở 16 Ω, chúng ta có thể sử dụng mạch nối tiếp và song song.
Cách mắc như sau:
Đặt R1 và R2 nối tiếp nhau: R12 = R1 + R2 = 10 + 10 = 20 ΩR3 nối song song với R12: R123 = 1/(1/R12 + 1/R3) = 1/(1/20 + 1/30) = 12 ΩR4 nối tiếp với R123: R1234 = R123 + R4 = 12 + 40 = 52 ΩTa có R1234 = 16 Ω, vậy cách mắc này đạt yêu cầu.
Sơ đồ mạch điện:
---[R1]---[R2]--- | | ---[R3]---[R4]---Trong sơ đồ trên, dấu --- biểu thị mạch nối tiếp và dấu | biểu thị mạch song song.

mình sẽ mô tả cách vẽ, bạn tự vẽ nhé:
C1: 3 điện trở nối tiếp
Rtđ=R1+R2+R3
C2: 3 điện trở song song
\(\dfrac{1}{Rtđ}\)=\(\dfrac{1}{R1}+\dfrac{1}{R2}+\dfrac{1}{R3}\)
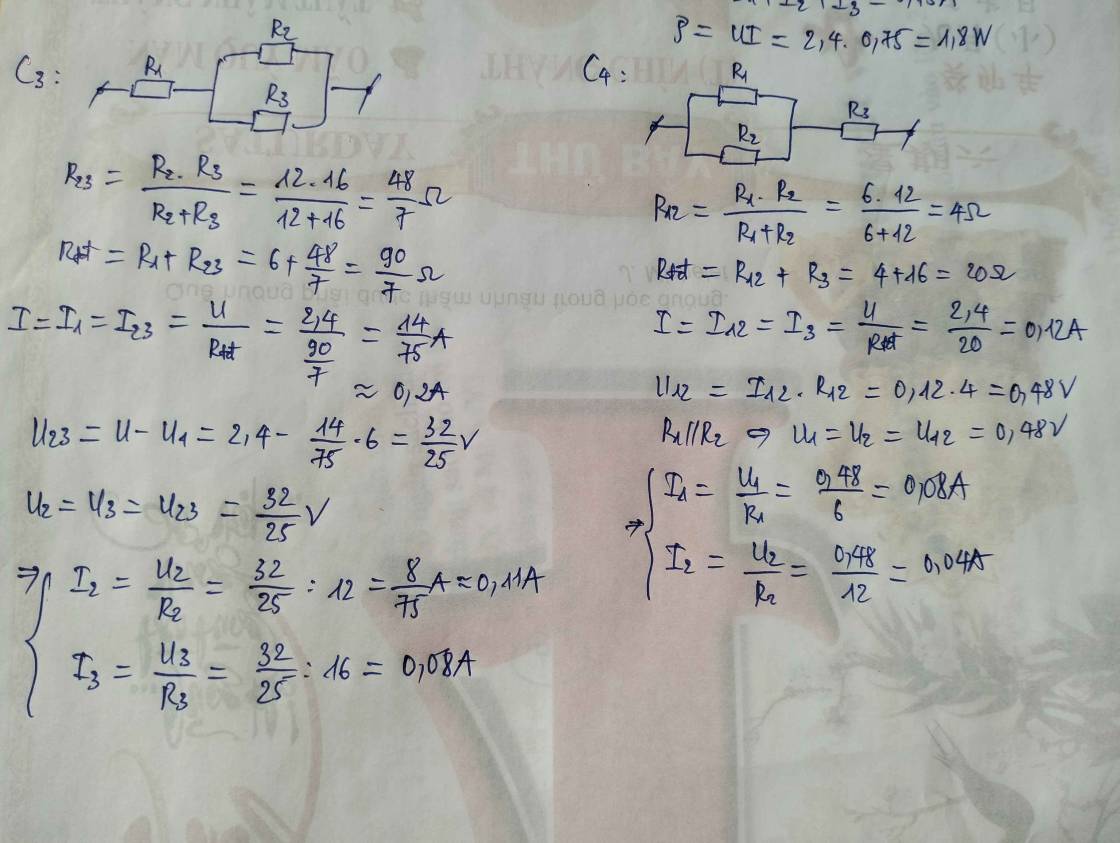
C3: R1 nt (R2//R3)
Rtđ=R1+(\(\dfrac{1}{R2}+\dfrac{1}{R3}\))
C4: (R1 nt R2)//R3
Rtđ=\(\dfrac{\left(R1+R2\right)R3}{R1+R2+R3}\)

C
B