TH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HD
Hà Đức Thọ
Admin
9 tháng 10 2015
Điện xoay chiều thú vị ở chỗ đó, chúng ta có thể dùng biến đổi đại số, dùng giản đồ véc tơ (tạm gọi là véc tơ thường - véc tơ buộc và véc tơ trượt), ngoài ra còn có thể dùng số phức để giải. Tùy từng bài toán và tùy từng kinh nghiệm của mỗi người thì sẽ biết nên làm theo cách nào cho hợp lí. Em hãy cứ làm nhiều bài tập điện xoay chiều thì em sẽ nhận ra điều đó.
Dùng giản đồ véc tơ thường thì hầu như dạng bài tập nào cũng giải được.
Còn véc tơ trượt là một biến thể của véc tơ thường (dựa vào tính chất cộng véc tơ trong toán học), làm cho hình vẽ đỡ rối hơn.
Còn nên dùng theo cách nào thì như mình nói tùy từng bài toán và kinh nghiệm của mỗi người. Kinh nghiệm của mình là những bài toán mà cho mối liên hệ các điện áp chéo nhau (VD: URL, URC,...) thì dùng véc tơ thường, trường hợp còn lại thì dùng véc tơ trượt.
NH
3
13 tháng 11 2021
Đừng nhắn linh tinh bạn nhé nhưng mình có chơi , tên là HR.KinhZZ
NM
2
6 tháng 1 2022
Hgjuyggrhf? 7? 6,kt65jujyufu4d5tfyj3a4yjtdy4h5stdgyxnthzrtjyx5y4strbxhrztgdyrttgutdytjxg5fy5cjyjc6yku6 7kug7ug7lgiuk kut7t ut6k uk6t uho887y 8y7 9 tốt tớ 7ct788 rc65t6 Chào x5d 44,43wz54e, r6 i. Ti7d5ud5u tr r66t k7k6k t7kl78y tùm lum 686t76u Chào 5 ít 7t y8oi67ty4e5y4e4e4y55ru6j từ từ 6 o8. 8yo 8yo ít ur6 Chào Chào e, 7. 5u t 5u 5u y7 em. em cũng cũng p787b09
Uhiy7b8poy7b8uy gg6i 877 y bị 785 bộ 7b8phiklibuyi86vi7vv7ioyvjytguu7guyfy6fftfc
VT
6 tháng 9 2018
Khi hệ vân giao thoa đã ổn định thì trung điểm I của S 1 S 2 lại luôn luôn là cực đại giao thoa. Do đó, ta phải có :
S 1 I = S 2 I = k λ /2 + λ /4 = (2k + 1) λ /4
S 1 S 2 = 2 S 1 I = (2k + 1) λ /2
Ban đầu ta đã có : S 1 S 2 = 8cm = 10 λ = 20 λ /2
Vậy chỉ cần tăng khoảng cách S 1 , S 2 thêm λ /2 tức là 0,4 cm.
Khi đó nếu không kể đường trung trực của S 1 S 2 thì có 20 gợn sóng hình hypebol (vì gợn sóng là quỹ tích những điểm dao động mạnh hơn cả).
VT
18 tháng 10 2019
Đáp án D
*Khoảng có bề rộng nhỏ nhất mà không có vân sáng nào quan sát được trên màn tương ứng nằm ở dưới phía liền kề khi có hai quang phổ chồng lên nhau
*Bây giờ chúng ta đi xác định phổ bậc bao nhiêu thì có sự chồng lên nhau.
Áp dụng công thức tính k nhanh:
Do khoảng bề rộng nhỏ nhất nên có hai quang phổ chồng lên nhau suy ra n=1.
. Như vậy ở phổ bậc bắt đầu có 3 sự trùng nhau nên dưới phổ bậc 3 là có khoảng tối nhỏ nhất. QP bậc 3 có một phần chồng với quang phổ bậc 4. Do đó QP bậc 2 và 3 không chồng lên nhau. (Quan sát hình 1).
Do đó 
Phương pháp tổng quát.
Ta lấy lấy vân sáng bậc k làm chuẩn. Từ đó chúng ta đi xác định k. Xác định được kmin tức là chúng ta đã biết được tại quang phổ bậc bao nhiêu bắt đầu có sự chồng lên nhau. Khi biết được từ quang phổ bậc bao nhiêu có sự chồng nhau thì bài toán trở nên vô cùng đơn giản.
Tại một vị trí có m quang phổ chồng lên nhau tức là có m vân sáng quan sát được
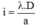
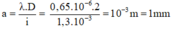
Tất nhiên là bằng 0, số j nhân vs 0 mà chả bằng 0. Nhưng còn về cái tin nhắn thì mình cũng muốn hỏi như thế