Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ bCó: a ⊥ c; m ⊥ c; C1̂ = 20o; A1̂ = 70o; B1̂ = 70o Điểm I là trung điểm của đoạn AB a) Chứng minh: a // b; c ⊥ b

a) Ta có MN vuông góc với AB ( do MN là đường trung trực của đoạn thẳng AB theo giả thuyết nên suy ra)
và đường thẳng m cũng vuông góc với đoạn thẳng AB ( theo giả thiết)
nên từ đó ta suy ra MN//m (đpcm)
b) Từ MN//m ta suy ra MIC=ICB (hai góc so le trong)
mà ICB= 60 độ => MIC=60 độ
c) Ta có HIB= HIN+NIB
Mặt khác HIN=MIC=60 độ ( so le trong)
và NIB=90 độ (gt)
suy ra HIB= 60+90=150 độ
d) Vì theo giả thiết ta có đường thẳng a đi qua C và song song với MN và điểm C lại nằm trên cùng một đường thẳng m với điểm B mà đường thẳng m lại song song với đường thẳng MN nên suy ra đường thẳng a trùng với đường thẳng m và đi qua B

- N nằm trên đường trung trực đoạn AB nên N cách đều AB hay AN =BN . Vậy tam giác ANB cân tại N
- Có : MN vuông góc AB & AC vuông góc AB ( GT) nên MN song song AC . Mà M là tđ AB nên MN là đg TB tam giac BAC . Suy ra N là tđ BC
Mình chưa học đường trung bình bạn giảii bằng cách khác đc ko.

a,Xét ΔMIA và ΔMIB có:
IA =IB (gt)
góc AIM = góc BIM (=90độ)
MI:cạnh chung
⇒ΔMIA = ΔMIB(c.g.c)

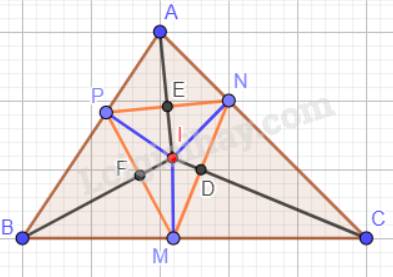
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.