Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số phần tử không gian mẫu là: C 40 4 = 91390 .
Số cách chọn 4 học sinh có cả học sinh xếp loại giỏi, khá, trung bình là:
C 10 2 . C 20 1 . C 10 1 + C 10 1 . C 20 2 . C 10 1 + C 10 1 . C 20 1 . C 10 2 = 37000
Số cách chọn 4 học sinh nam có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 9 1 . C 6 1 + C 5 1 . C 9 2 . C 6 1 + C 5 1 . C 9 1 . C 6 2 = 2295
Số cách chọn 4 học sinh nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
C 5 2 . C 11 1 . C 4 1 + C 5 1 . C 11 2 . C 4 1 + C 5 1 . C 11 1 . C 4 2 = 1870
Số cách chọn 4 học sinh có cả nam, nữ có cả học sinh xếp loại giỏi, khá, trung bình là:
37000 - 2295 - 1870 = 32835
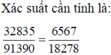

Gọi A là biến cố : "4 học sinh được chọn có đủ học sinh giỏi, học sinh khá và học sinh trung bình"
Số phần tử không gian mẫu \(\left|\Omega\right|=C^4_{33}=40920\)
Ta có các trường hợp được chọn sau :
(1) Có 2 học sinh giỏi, 1 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^2_{10}.C^1_{11}.C^1_{12}=5940\).
(2)Có 1 học sinh giỏi, 2 học sinh khá và 1 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^2_{11}.C^1_{12}=6600\).
(3)Có 1 học sinh giỏi, 1 học sinh khá và 2 học sinh trung bình. Số cách chọn là : \(C^1_{10}.C^1_{11}.C^2_{12}=7260\).
Ta được \(\left|\Omega_A\right|=5940+6600+7260=19800\)
Do đó : \(P\left(A\right)=\frac{\left|\Omega_A\right|}{\left|\Omega\right|}=\frac{15}{31}\)

Có 2 bạn giỏi văn , 7 bạn giỏi toán, 3 bạn giỏi cả 2 môn
Có 2C1.7C1 =14 ( cách )

Đáp án B
Xác suất bằng C 9 2 + C 10 2 + C 3 2 C 22 2 = 4 11 .

Đáp án B.
Số cách chọn 5 em học sinh từ 8 học sinh trên là ![]() cách
cách
- Để chọn 5 em thỏa mãn bài ra, ta xét các trường hợp sau
+) 1 nam khối 11, 1 nữ khối 12 và 3 nam khối 12 có ![]() cách
cách
+) 1 nam khối 11, 2 nữ khối 12 và 2 nam khối 12 có ![]() cách
cách
+) 2 nam khối 11, 1 nữ khối 12 và 2 nam khối 12 có ![]() cách
cách
+) 2 nam khối 11, 2 nữ khối 12 và 1 nam khối 12 có ![]() cách
cách
- Số cách chọn 5 em thỏa mãn bài ra là:
![]() cách
cách
Vậy xác suất cần tính là: ![]()
Gọi chung 2 loại học sinh khá và trung bình là K và học sinh giỏi là G
Các trường hợp thuận lợi: KKGG; KGGG; GKGG; GGGG
Xác suất:
\(P=\frac{C_{10}^2}{C_{15}^2}.\frac{C_5^2}{C_{13}^2}+\frac{C_{10}^1}{C_{15}^1}.\frac{C_5^3}{C_{14}^3}+\frac{C_5^1}{C_{15}^1}.\frac{C_{10}^1}{C_{14}^1}.\frac{C_4^2}{C_{13}^2}+\frac{C_5^4}{C_{15}^4}=\frac{2}{21}\)