Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Chú ý 4 cạnh khác nhau
Có C 6 4 cách chọn 4 màu khác nhau. Từ mỗi bộ 4 màu thì có 4! = 24 cách tô màu khác nhau.
Có C 6 3 cách chọn 3 màu khác nhau. Từ mỗi bộ 3 màu, có 4.3 = 12 cách tô.
Có C 6 2 cách chọn 2 màu khác nhau khi đó có: 2.1 = 2 cách tô.
Tổng cộng: 24 . C 6 4 + 4 . 3 C 6 3 + 2 . C 6 2 = 630 cách.

Ta có: \({u_1} = 1;{u_2} = 1;{u_3} = 2;{u_4} = 3;{u_5} = 5;{u_6} = 8;{u_7} = 13;{u_8} = 21\)
Ta có:
\(\begin{array}{l}{u_3} = 2 = {u_2} + {u_1}\\{u_4} = 3 = {u_3} + {u_2}\\{u_5} = 5 = {u_4} + {u_3}\\{u_6} = 8 = {u_5} + {u_4}\\{u_7} = 13 = {u_6} + {u_5}\\{u_8} = 21 = {u_7} + {u_6}\end{array}\)
Ta thấy dãy số này kể từ số hạng thứ 3 bằng tổng của hai số hạng đứng trước nó.
Vậy dãy số này có công thức truy hồi là:
\(\left\{ \begin{array}{l}{u_1} = 1;{u_2} = 1\\{u_n} = {u_{n - 1}} + {u_{n - 2}}\left( {n \ge 3} \right)\end{array} \right.\)

Chọn D
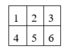
+ Tô màu ô vuông số 2: có C 3 2 cách chọn 2 trong 3 màu, có C 4 2 cách tô 2 màu đó lên 4 cạnh. Vậy có C 3 2 C 4 2 = 18cách.
+ Tô màu ô vuông số 1,5,3: có C 2 1 cách chọn màu còn lại, có C 3 2 cách tô màu còn lại lên 3 cạnh còn lại của 1 hình vuông. Vậy có ( C 2 1 C 3 2 ) 3 = 6 3 cách
+ Tô màu ô vuông số 4,6: Mỗi 1 hình vuông có 2 cách tô màu. Vậy có 2 2 = 4cách.
Vậy có 18. 6 3 .4 = 15552 cách thỏa mãn.

Đáp án D
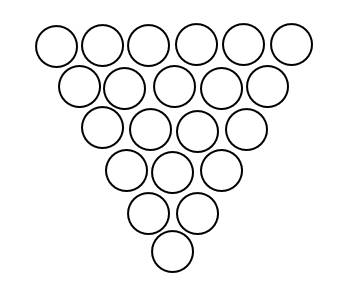
Lấy 2 đinh tô màu đỏ trong 6 điểm có C 6 2 cách
Lấy 1 đỉnh tô màu xanh trong 4 điểm có cách
Suy ra số tam giác tạo thành có 2 đỉnh tô màu đỏ là
C 6 2 . C 4 1 = 60
Vậy xác suất cần tính là
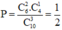



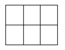

a) đặc tên của các ô trên là : \(ô_1\) ; \(ô_2\) ; \(ô_3\) ; \(ô_4\) \(\Rightarrow\) ta có
+ đối với \(ô_1\) ta có 6 cách tô
+ đối với \(ô_2\) ta có 6 cách tô
+ đối với \(ô_3\) ta có 6 cách tô
+ đối với \(ô_4\) ta có 6 cách tô
áp dụng qui tắc nhân \(\Rightarrow\) ta có \(6.6.6.6=1296\) cách tô màu cho 4 ô tròn
vậy có \(1296\) cách tô màu cho 4 ô tròn
b) vì các ô phải đôi 1 khác nhau nên màu của \(ô_1\neô_2\neô_3\neô_4\) \(\Rightarrow\) ta có :
+ đối với \(ô_1\) ta có 6 cách tô
+ đối với \(ô_2\) ta có 5 cách tô
+ đối với \(ô_3\) ta có 4 cách tô
+ đối với \(ô_4\) ta có 3 cách tô
áp dụng qui tắc nhân \(\Rightarrow\) ta có : \(6.5.4.3=360\) cách tô màu cho 4 ô tròn thỏa mãn điều kiện bài toán
vậy có \(360\) cách tô màu cho 4 ô tròn sao cho các ô phải đôi 1 khác nhau