NN
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
S
25 tháng 10 2020
thấy ngay \(p_6>2\text{ do đó: }VP\equiv1\left(\text{mod 8}\right)\text{ từ đó suy VP cũng đồng dư với 1 mod 8}\)
có bổ đề SCP LẺ chia 8 dư 1 do đó:
trong 5 số: \(p_1;p_2;...;p_5\text{ có 4 số chẵn; 1 số lẻ không mất tính tổng quát giả sử: }p_5\text{ lẻ}\Rightarrow16+p_5^2=p_6^2\text{(đơn giản)}\)
S
25 tháng 10 2020
\(p+1=2a^2;p^2+1=2b^2\Rightarrow p\left(p-1\right)=2\left(b-a\right)\left(b+a\right)\)
\(\text{thấy ngay p lẻ}\Rightarrow UCLN\left(p^2+1,p+1\right)=1;\Rightarrow\left(a,b\right)=1\Rightarrow\left(b-a,a+b\right)=1\)
thấy ngay p>b-a nên: \(p=a+b;p-1=2a-2b\text{ hay:}a+b=2b-2a+1\Leftrightarrow3a=b+1\)
đến đây thì đơn giản
CM
17 tháng 5 2017
Đáp án D
Hệ phương trình đối xứng loại 1 với cách đặt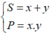 
điều kiện
S
2
≥
4
P
⇔
S
2
-
4
P
≥
0
21 tháng 8 2016
Xét tứ giác ABCD có cạnh đối diện AD và BC cắt nhau tại O. Gọi D1 và C1 lần lượt là các điểm đối xứng của C và D qua O. Khi đó có :
\(AC_1=AC,BD_1=BD,C_1D_1=CD\)
Áp dụng định lí ta có:
\(ABD_1C_1:AD_1\perp BC_1\Leftrightarrow AB^2+C_1D_1^2=AC^2_1+BD^2_1\)
\(\Rightarrow AD\perp BC\Leftrightarrow AB^2+CD^2=AC^2+BD^2\)
NV
30 tháng 6 2018
ta đx biết nếu G là trọng tâm của ABC thì
GA+GB+GC=0
AA' =AG+GG'+G'A'
BB'=BG+GG'+G'B'
CC'=CG+GG'+G'C"
==> AA'+BB'+CC'=(AG+BG+CG)+3GG'+(G'A'+G'B'+G...
ĐPCM
dk cần và đủ để 2 tam giác có cùng trọng tâm là
AA'+BB'+CC' =0
c/m:
dk cần:AA'+BB'+CC'=0 thì ABC và A'B'C' cùng trọng tâm
vì AA'+BB'+CC'=3GG'
==> GG'=0 ==> G trùng G'
dk đủ: G trùng G' thì AA'+BB'+CC'=0
AA'+BB'+CC'=3GG'
mà GG' =0 ==> AA'+BB'+CC'=0 ĐPCM
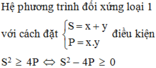
Thê p = 3 vào thì ta được
\(\hept{\begin{cases}p=3\\8p^2+1=73\end{cases}}\) là 2 số nguyên tố.
Xét \(p=3k⋮3\left(k\ne1\right)\)nên không phải số nguyên tố.
Xét \(p=3k+1\)
\(\Rightarrow8\left(3k+1\right)^2+1=72k^2+48k+9⋮3\)nên không phải số nguyên tố.
Xét \(p=3k+2\)
\(\Rightarrow8\left(3k+2\right)^2+1=72k^2+96k+33⋮3\)
Vậy để \(p,8p^2+1\)đồng thời là 2 số nguyên tố thì \(p=3\)