Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt AB = c; BC = a; AC = b
sinA = sinB . cosC + sinB . cosB
⇔ 2R. sinA = 2R. sinB . cosC + 2R. sinC . cosB
⇔ a = b. cosC + c. cosB
⇔ a2 = ab . cosC + ac . cosB
⇔ a2 = \(\dfrac{a^2+b^2-c^2}{2}+\dfrac{a^2+c^2-b^2}{2}\)
⇔ a2 = a2 (cái này là hiển nhiên rồi!!)
Vậy khi điều cần chứng minh là một mệnh đề tương đương với một mệnh đề đúng thì nó là mệnh đề đúng
Cách làm : Viết ngược từ dưới lên bạn nhá :))

Trong một tam giác thì tổng các góc là 1800 :
+
+
= 1800 =>
= -1800 – (
+
)
và (
+
) là 2 góc bù nhau, do đó:
a) sinA = sin[1800 – ( +
)] = sin (B + C)
b) cosA = cos[1800 – ( +
)] = -cos (B + C)

a) Áp dụng hệ quả của định lí côsin trong tam giác ta có:
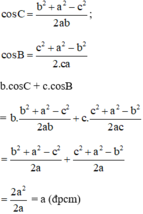
b) Theo định lí tổng ba góc của tam giác ta có:
A + B + C = 180º
⇒ sin A = sin [180º – (B – C)]= sin (B + C) = sinB.cos C + cosB. sinC (đpcm)
c) Theo định lí sin trong tam giác ABC, ta có:
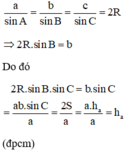

Theo đl sin có:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\Rightarrow b=a\dfrac{sinB}{sinA};c=\dfrac{sinC}{sinA}.a\)
Mà `b+c=2a`
\(\Rightarrow a\dfrac{sinB}{sinA}+a\dfrac{sinC}{sinA}=2a\\ \Rightarrow\dfrac{sinB}{sinA}+\dfrac{sinC}{sinA}=2\\ \Leftrightarrow sinB+sinC=2sinA\)
Chọn B

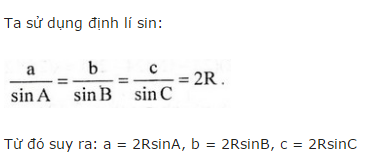
\(A+B+C=180^0\Rightarrow sinA=sin\left(180^0-\left(B+C\right)\right)=sin\left(B+C\right)=sinBcosC+sinC.cosB\)