Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có g → / = g → + a → q t mà trọng lượng của vật khi thang máy chuyển động là P / = m g /
a. Khi thang máy đứng yên a = 0 m / s 2
⇒ N = P = m g = 10.10 = 100 N
b. Đi lên nhanh dần đều với gia tốc 1 m / s 2
a → q t ↓ ↓ g → ⇒ g / = g + a q t
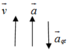
⇒ g / = 10 + 2 = 12 m / s 2 ⇒ N = P / = m g / = 10.12 = 120 N
c. Đi lên chậm dần đều với gia tốc 2 m / s 2
a → q t ↑ ↓ g → ⇒ g / = g − a q t
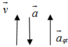
⇒ g / = 10 − 2 = 8 m / s 2 ⇒ N = P / = m g / = 10.8 = 80 N
d. Đi xuống nhanh dần đều với gia tốc 2 m / s 2
a → q t ↑ ↓ g → ⇒ g / = g − a q t
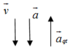
⇒ g / = 10 − 2 = 8 m / s 2 ⇒ N = P / = m g / = 10.8 = 80 N
e. Đi xuống chậm dần đều với gia tốc 2 m / s 2
a → q t ↓ ↓ g → ⇒ g / = g + a q t
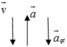
⇒ g / = 10 + 2 = 12 m / s 2 ⇒ N = P / = m g / = 10.12 = 120 N
f. Chuyển động thẳng đều 2m/s
Vì thang máy chuyển động thẳng đều nên
a = 0 m / s 2 ⇒ N = P = m g = 10.10 = 100 N

Tóm tắt:
\(v_0=0\) m/s
v=4 m/s
\(t_0=0\) s
\(t_1=4\) s
\(t_2=5\) s
\(t_3=8\) s
\(s=?\)km
Giải
Gia tốc của thang máy trong giai đoạn 1 là
\(a=\dfrac{\Delta v}{\Delta t}=\dfrac{v-v_0}{t_1-t_0}=\dfrac{4-0}{4-0}=1\)(m/s2)
Quãng đường thang máy chuyển động trong giai đoạn 1 là
\(s_1=v_0t_1+\dfrac{1}{2}at_1^2=0\cdot4+\dfrac{1}{2}\cdot1\cdot4^2=8\left(m\right)\)
Quãng đường thang máy chuyển động trong giai đoạn 2 là
\(s_2=v\cdot t_2=4\cdot5=20\left(m\right)\)
Gia tốc của thang máy trong giai đoạn 2 là
\(a'=\dfrac{\Delta v'}{\Delta t'}=\dfrac{v-v_0}{t_3}=\dfrac{4-0}{8}=\dfrac{1}{2}\)(m/s2)
Quãng đường thang máy chuyển động trong giai đoạn 3 là
\(s_3=v_0t_3+\dfrac{1}{2}a't_3^2=0\cdot8+\dfrac{1}{2}\cdot\dfrac{1}{2}\cdot8^2=16\left(m\right)\)
Quãng đường di chuyển dc của thang máy là
\(s_1+s_2+s_3=8+20+16=44\left(m\right)\)

a, Ngoại lực tác dụng lên thang máy là trọng lực và kéo của động cơ thang máy. Áp dụng định lý về động năng ta có: Wđ1 – Wđ0 = A F 1 → + A P 1 →
Mà Wđ1 = m . v 1 2 2 , Wđ0 = m . v 0 2 2 = 0 ;
A P 1 → = − P . s 1 = − m . g . s 1 ( A P → 1 < 0 )
Vì thang máy đi lên
⇒ A F 1 = m . v 1 2 2 + m . g . s 1 = 1 2 .1000.5 2 + 1000.10.5 = 62500 J
b, Vì thang máy chuyển động đều, lực kéo của động cơ cân bằng với trọng lực P → : F 2 → + P → = 0 . Công phát động của động cơ có độ lớn bằng công cản A F 2 → = − A P → với A P = − P . s 2 = − m . g . s 2
=> AF2 = mgs2 do đó công suất của động cơ thang máy trên đoạn đường s2 là:
℘ 2 = A F 2 t = m . g . s 2 t = m . g . v 2 = m . g . v 1 ⇒ ℘ 2 = 1000.10.5 = 50000 ( W ) = 50 ( k W ) .
c, Ngoại lực tác dụng lên thang máy là trọng lực P → và lực kéo F 3 → của động cơ.
Áp dụng định lí động năng ta có: Wđ3 – Wđ2 = AF3 + Ap’
Mà Wđ3 = m . v 3 2 2 = 0 ; Wđ2 = m v 2 2 2 (v2 = v1 = 5m/s); Ap = - Ps3 = - mgs3
Công của động cơ trên đoạn đường s3 là: AF3 = mgs3 - m v 2 2 2 = 37500J
Áp dụng công thức tính công ta tìm được lực trung bình do động cơ tác dụng lên thang máy trên đoạn đường s3: F 3 ¯ = A F 3 s 3 = 37500 5 = 7500 N