HT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NP
1
13 tháng 5 2020
Cho\(\Delta ABC~\Delta DEF\) với tỉ số đồng dạng:\(\frac{3}{2}\)
Vì\(\Delta ABC~DEF\) theo tỉ số\(\frac{3}{2}\) nên ta có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{3}{2}\)
Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{AB}{DE}=\frac{AC}{DF}=\frac{BC}{EF}=\frac{AB+AC+BC}{DE+DF+EF}=\frac{3}{2}\)
Suy ra:\(\frac{AB+AC+BC}{DE+DF+EF}=\frac{3}{2}\)
Vậy \(\frac{P_{ABC}}{P_{DEF}}=\frac{3}{2}\)
Hay tỉ số chu vi của 2 tam giác đồng dạng bằng nhau
P:chu vi
#hoktot<3#
CM
28 tháng 1 2017
Vì △ A'B'C' đồng dạng △ ABC theo tỉ số k nên ta có:
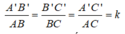
Theo tính chất dãy tỉ số bằng nhau, ta có:
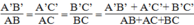
Suy ra: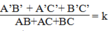 
Vậy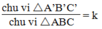 
BM
1
14 tháng 2 2022
Gọi chu vi của tam giác ABC là C1, chu vi của tam giác DEF là C2
và ΔABC∼ΔDEF
=>AB/DE=BC/EF=AC/DF
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{DE}=\dfrac{BC}{EF}=\dfrac{AC}{DF}=\dfrac{AB+BC+AC}{DE+EF+DF}=\dfrac{C_1}{C_2}\)
Do đó: Tỉ số chu vi bằng tỉ số đồng dạng
8 tháng 4 2020
1/
Ta có: \(\frac{12}{16}=\frac{9}{12}=\frac{15}{20}=\frac{3}{4}\Leftrightarrow\frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{FD}\)
suy ra Tam giác ABC đồng dạng với tam giác DEF
Nên \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{DEF}\\\widehat{ACB}=\widehat{DFE}\\\widehat{BAC}=\widehat{EDF}\end{matrix}\right.\) (2 góc tương ứng)
10 tháng 5 2023
AB/sinC=2R
A'B'/sinC'=2R'
mà AB/A'B'=k
và goc C=góc C'
nên 2R/2R'=AB/A'B'=k
=>R/R'=k(Đpcm)
Giả sử ta có tam giác thứ nhất có các cạnh là a; b; c đồng dạng với tam giác có các cạnh tương ứng là m; n; p
Gọi chu vi tg thứ nhất là C1; chu vi tam giác thứ 2 là C2
=> a/m=b/n=c/p (tỷ số đồng dạng) theo t/c dãy tỷ số bằng nhau
=> a/m=b/n=c/p=(a+b+c)/(m+n+p)=C1/C2