Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{3ac}{a^3b}=\dfrac{3c}{a^2b}\)
\(\dfrac{6c}{2a^2b}=\dfrac{3c}{a^2b}\)
\(\Rightarrow\dfrac{3ac}{a^3b}=\dfrac{6c}{2a^2b}\)
b) \(\dfrac{3ab-3b^2}{6b^2}=\dfrac{3b\left(a-b\right)}{6b^2}=\dfrac{a-b}{2b}\left(dpcm\right)\)
`a, (3ac)/(a^3b) = (3c)/(a^2b)`
`(6c)/(2a^2b) = (3c)/(a^2b)`
Vậy hai phân thức `=` nhau
`b, (3ab-3b^2)/(6b^2) = (3b(a-b))/(6b^2) = (a-b)/(2b)`
Vậy hai phân thức `=` nhau

a: \(\dfrac{a+b}{ab}=\dfrac{a\left(a+b\right)}{a^2b}=\dfrac{a^2+ab}{a^2b}\)
\(\dfrac{a-b}{a^2}=\dfrac{ab-b^2}{a^2b}\)
b: \(A+B=\dfrac{a^2+ab+ab-b^2}{a^2b}=\dfrac{a^2+2ab-b^2}{a^2b}\)
\(A-B=\dfrac{a^2+ab-ab+b^2}{a^2b}=\dfrac{a^2+b^2}{a^2b}\)

d: \(\Leftrightarrow\dfrac{\left(x+2\right)^2}{\left(x+2\right)\left(x-2\right)}=\dfrac{\left(x+1\right)\left(x+2\right)}{A}\)
hay A=x-2

Ta có: a+b+c=0
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=-c\\b+c=-a\\a+c=-b\end{matrix}\right.\)
Ta có: \(P=\dfrac{ab^2}{a^2+b^2-c^2}+\dfrac{bc^2}{b^2+c^2-a^2}+\dfrac{ca^2}{c^2+a^2-b^2}\)
\(=\dfrac{ab^2}{\left(a+b\right)^2-c^2-2ab}+\dfrac{bc^2}{\left(b+c\right)^2-a^2-2bc}+\dfrac{ca^2}{\left(c+a\right)^2-b^2-2ac}\)
\(=\dfrac{ab^2}{\left(a+b+c\right)\left(a+b-c\right)-2ab}+\dfrac{bc^2}{\left(b+c+a\right)\left(b+c-a\right)-2bc}+\dfrac{ca^2}{\left(c+a+b\right)\left(c+a-b\right)-2ac}\)
\(=\dfrac{ab^2}{-2ab}+\dfrac{bc^2}{-2bc}+\dfrac{ca^2}{-2ac}\)
\(=\dfrac{-ab\cdot b}{2ab}+\dfrac{-bc^2}{2bc}+\dfrac{-ca^2}{2ac}\)
\(=\dfrac{-b}{2}+\dfrac{-c}{2}+\dfrac{-a}{2}=\dfrac{-\left(a+b+c\right)}{2}=\dfrac{0}{2}=0\)

Ta có: \(\left(a^2-a+1\right)\left(a+2\right)\)
\(=a^3+2a^2-a^2-2a+a+2\)
\(=a^3+a^2-a+2\)(1)
Ta có: \(\left(a^2+3a-1\right)\left(a-2\right)\)
\(=a^3-2a^2+3a^2-6a-a+2\)
\(=a^3+a^2-7a+2\)(2)
Từ (1) và (2) suy ra \(\dfrac{a^2-a+1}{a-2}\ne\dfrac{a^2+3a-1}{a+2}\)

a) 32x−332x−3 và 3x+62x2+x−63x+62x2+x−6
Cách 1: Dùng định nghĩa hai phân thức bằng nhau.
32x−332x−3= 3x+62x2+x−63x+62x2+x−6
Vì : 3(2x2+x−6)=6x2+3x−183(2x2+x−6)=6x2+3x−18
=6x2+12x−9x−186x2+12x−9x−18
=2x(3x+6)−3(3x+6)2x(3x+6)−3(3x+6)
=(2x−3)(3x+6)(2x−3)(3x+6)
Cách 2: Rút gọn phân thức
3x+62x2+x−6=3(x+2

Bài 1: (Sgk/36):
a. \(\dfrac{5y}{7}\)=\(\dfrac{20xy}{28x}\) vì
5y . 28x = 140xy
7 . 20xy = 140xy
=> 5y . 28x = 7 . 20xy
Vậy \(\dfrac{5y}{7}\)=\(\dfrac{20xy}{28x}\)
b. \(\dfrac{3x\left(x+5\right)}{2\left(x+5\right)}\)=\(\dfrac{3x}{2}\) vì
3x . 2(x+5) = 6x2+30x
2 . 3x(x+5) = 6x2+30x
=> 3x . 2(x+5) = 2 . 3x(x+5)
Vậy \(\dfrac{3x\left(x+5\right)}{2\left(x+5\right)}\)=\(\dfrac{3x}{2}\)
c. \(\dfrac{x+2}{x-1}\)=\(\dfrac{\left(x+2\right)\left(x+1\right)}{x^2-1}\) vì
(x+2) (x2-1) = (x+2) (x-1) (x-1)
=> (x+2) (x2-1) = (x-1) (x+2) (x+1)
Vậy \(\dfrac{x+2}{x-1}\)=\(\dfrac{\left(x+2\right)\left(x+1\right)}{x^2-1}\)
d. \(\dfrac{x^2-x-2}{x+1}\)=\(\dfrac{x^2-3x+2}{x-1}\)
(x-1) (x2-x-2) = x3-2x2-x+2
(x+1) (x2-3x+2) = x3-2x2-x+2
=> (x-1) (x2-x-2) = (x2-3x+2) (x+1)
Vậy \(\dfrac{x^2-x-2}{x+1}\)=\(\dfrac{x^2-3x+2}{x-1}\)

\(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}=0\Leftrightarrow ab+bc+ca=0\Rightarrow\left\{{}\begin{matrix}bc=-ab-ac\\ab=-bc-ac\\ac=-ab-bc\end{matrix}\right.\)
\(M=\dfrac{1}{a^2+bc-ab-ac}+\dfrac{1}{b^2+ac-ab-bc}+\dfrac{1}{c^2+ab-bc-ac}\)
\(=\dfrac{1}{a\left(a-b\right)-c\left(a-b\right)}+\dfrac{1}{b\left(b-c\right)-a\left(b-c\right)}+\dfrac{1}{c\left(c-a\right)-b\left(c-a\right)}\)
\(=\dfrac{1}{\left(a-b\right)\left(a-c\right)}-\dfrac{1}{\left(a-b\right)\left(b-c\right)}+\dfrac{1}{\left(a-c\right)\left(b-c\right)}\)
\(=\dfrac{b-c-\left(a-c\right)+a-b}{\left(a-b\right)\left(b-c\right)\left(a-c\right)}=0\)
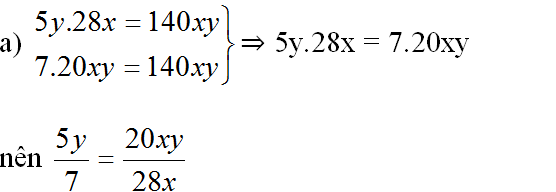
`(a^2-b^2)/(a^2b + ab^2) = ((a-b)(a+b))/(ab(a+b)) = (a-b)/(ab)`.
`(a-b)/(ab) = ((a-b)(a+b))/(ab(a+b)) = (a^2-b^2)/(ab(a+b))`