
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu trên đề sai
\(\frac{2\sqrt{3+\sqrt{5-\sqrt{13+\sqrt{48}}}}}{\sqrt{6}+\sqrt{2}}\)
\(=\frac{2\sqrt{3+\sqrt{5-\sqrt{13+4\sqrt{3}}}}}{\sqrt{6}+\sqrt{2}}\)
\(=\frac{2\sqrt{3+\sqrt{4-2\sqrt{3}}}}{\sqrt{6}+\sqrt{2}}\)
\(=\frac{2\sqrt{2+\sqrt{3}}}{\sqrt{6}+\sqrt{2}}=\sqrt{2}\frac{\sqrt{4+2\sqrt{3}}}{\sqrt{6}+\sqrt{2}}\)
\(=\frac{\sqrt{2}\left(\sqrt{3}+1\right)}{\sqrt{6}+\sqrt{2}}=1\)
Vậy nó là số nguyên

Ta có:
\(a+b+c=4\)
\(\Rightarrow\) \(a< 4\)
\(\Rightarrow\) \(a^4< 4a^3\) (do \(a>0\) nên \(a^3>0\) )
Do đó, \(a^3>\frac{a^4}{4}\) hay nói cách khác, \(\sqrt[4]{a^3}>\sqrt[4]{\frac{a^4}{4}}=\frac{a}{\sqrt[4]{4}}\) \(\left(1\right)\)
Từ đó, ta cũng tương tự thiết lập được: \(\sqrt[4]{b^3}>\frac{b}{\sqrt[4]{4}}\) \(\left(2\right)\) và \(\sqrt[4]{c^3}>\frac{c}{\sqrt[4]{4}}\) \(\left(3\right)\)
Cộng từng vế các bđt \(\left(1\right);\) \(\left(2\right);\) và \(\left(3\right)\) ta có:
\(\sqrt[4]{a^3}+\sqrt[4]{b^3}+\sqrt[4]{c^3}>\frac{a+b+c}{\sqrt[4]{4}}=\frac{4}{\sqrt[4]{4}}=2\sqrt{2}\)

Có \(a+1+1\ge3\sqrt[3]{a}\)
\(b+1+1\ge3\sqrt[3]{b}\)
\(\Rightarrow a+b+1+1+1+1\ge3\left(\sqrt[3]{a}+\sqrt[3]{b}\right)\)
\(\Rightarrow3\left(\sqrt[3]{a}+\sqrt[3]{b}\right)\le6\)
\(\Rightarrow\sqrt[3]{a}+\sqrt[3]{b}\le2\)
"=" tại a=b=1

Đặt \(\sqrt[4]{a}=x;\sqrt[4]{b}=y;\sqrt[4]{c}=z\)
Cần chứng minh
\(\sqrt[4]{a}+\sqrt[4]{b}>\sqrt[4]{c}=\sqrt[4]{a+b}\)
\(\Rightarrow\left(x^3+y^3\right)^4>\left(x^4+y^4\right)^3\)
Rôi phân phối ra là thấy

\(\frac{a^2+b^2}{a-b}=\frac{\left(a-b\right)^2+2ab}{a-b}=a-b+\frac{2ab}{a-b}=a-b+\frac{12}{a-b}\ge2\sqrt{12}=4\sqrt{3}\left(Cauchy\right)\)

a) (căn 3-1)^2 = (căn 3)^2 - 2.căn 3.1 + 1^2 (theo hẳng đẳng thức bình phương 1 hiệu)
= 3 - 2.căn 3 +1 = 4 - 2.căn 3
b) Theo câu a ta có 4-2.căn 3 = (căn 3-1)^2
=> căn của 4-2.căn 3 = căn 3-1 (khai phương ra ah)
=> căn của 4-2.căn 3 - căn 3 = căn 3 -1 - căn 3= -1
(sr bạn mk ko bt vt dấu căn nên hơi khó hỉu =.=)
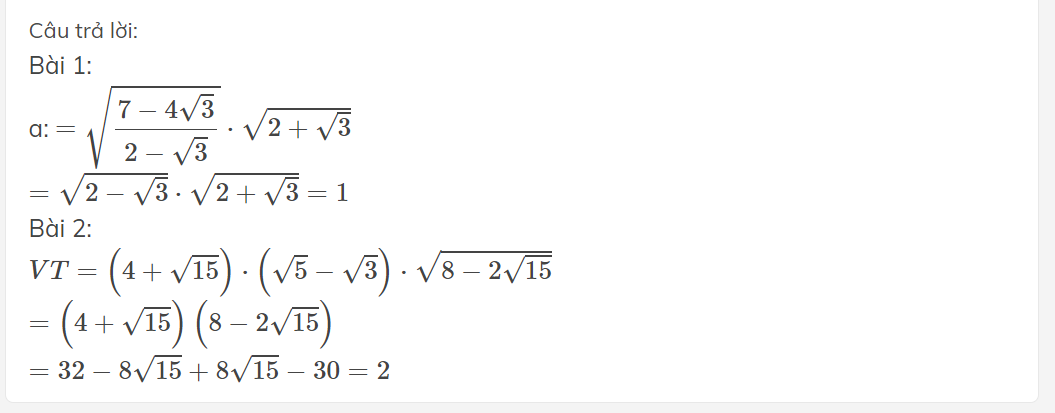
Đề thiếu VP nha b:)
Bạn ơi
Chứng minh gì vậy bạn
( mà xin lỗi vì mình mới lớp 6 )