Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/Giả sử trong 1 tam giác có 2 hóc tù thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=>trong 1 tam giác chỉ có duy nhất 1 góc tù
2/Trong 1 tam giác nếu góc nhỏ nhất bằng 60 độ thì tổng 3 góc của tam giác đó sẽ lớn hơn 180 độ
=> trong một tam giác góc nhỏ nhất không thể lớn hơn 60 độ
3/Xét tam giác AMB = tam giác AMC (c.c.c)
=> góc BMA = góc CMA
Mặt khác góc BMA + góc CMA = 180 độ
=> góc BMA = góc CMA = 90 độ
=> AM vuông góc BC
=> AM là đường cao của tam giác hạ từ đỉnh A
Tam giác BMA = tam giác CMA
=> góc BAM = góc CAM
=> AM là tia phân giác của góc A


Giả sử \(\Delta\)DEF đều
\(\Rightarrow\widehat{EDF}=60^0\)
Lại có ^DHC = 900 (gt) nên ^BCK = 300
Mà CK là phân giác của ^C nên \(\widehat{KCA}=30^0\)và ^ACB = 600
Kết hợp với \(\widehat{IEC}=60^0\)(đối đỉnh với ^DEF = 600)
=> \(\widehat{EIC}=90^0\)
\(\Delta ABC\)có BI là trung tuyến đồng thời là đường cao nên \(\Delta ABC\)cân tại B
Mà ^ACB = 600 nên \(\Delta ABC\) đều
=> Ba đường AH, BI, CK đồng quy
=> D,E,F trùng nhau
Vậy DEF không thể là tam giác đều (đpcm)


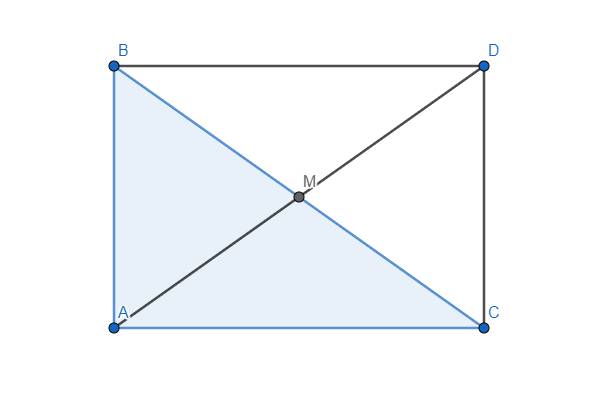
Trên tia đối của tia MA lấy điểm D sao cho \(MD=MA\). Khi đó xét 2 tam giác MAB và MDC, ta có \(MA=MD\) (cách vẽ), \(\widehat{AMB}=\widehat{DMC}\) và \(MB=MC\) (do AM là đường trung tuyến của tam giác ABC)
\(\Rightarrow\Delta MAB=\Delta MDC\left(c.g.c\right)\) \(\Rightarrow\widehat{MAB}=\widehat{MDC}\) \(\Rightarrow AB//CD\). Mà \(AB\perp AC\) nên \(AC\perp CD\) hay \(\widehat{ACD}=90^o\)
Đồng thời ta cũng có \(AB=CD\)
Xét 2 tam giác ABC và CDA, có AC là cạnh chung, \(\widehat{BAC}=\widehat{DCA}\left(=90^o\right)\) và \(AB=CD\left(cmt\right)\), suy ra \(\Delta ABC=\Delta CDA\left(c.g.c\right)\) \(\Rightarrow BC=AD\)
\(\Rightarrow\dfrac{1}{2}BC=\dfrac{1}{2}AD\) \(\Rightarrow MB=MA\)
Từ đó ta có \(MA=MB=MC=MD\), suy ra đpcm.
Đúng rồi bạn mà đề bài là gì vậy bạn
c tui nha
thanks
sin lôi nha de là chứng minh ràng