Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi độ dài ba cạnh của tam giác lần lượt là a, b, c ( a, b, c > 0 )
a3=b4=c5a3=b4=c5 và c−a=4c−a=4
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
a3=b4=c5=c−a5−3=42=2a3=b4=c5=c−a5−3=42=2
⇒⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩a3=2⇒a=6b4=2⇒b=8
Gọi độ dài 3 cạnh của hình tam giác lll : x; y; z (cm)
(đk : x; y; z ∈ N*)
Theo đề bài ta có :
x/3 = y/4 = z/5 và x + y - z = 4
Áp.........................ta có:
x/3 = y/4 = z/5 = (x + y - z)/(3 + 4 - 5) = 4/2 = 2
=> x/3 = 2 => x = 6
y/4 = 2 => y = 8
z/5 = 2 => z = 10
Chu vi hình tam giác là:
6 + 8 + 10 = 24 (cm)
Vậy . . .

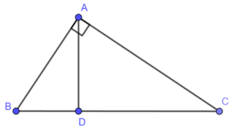
Xét hai tam giác vuông DAC và DBA ,ta có:
∠ (ADC) = ∠ (BDA) = 90 0
∠ C = ∠ (DAB) (hai góc cùng phụ ∠ B )
Suy ra: △ DAC đồng dạng △ DBA (g.g)
Suy ra: 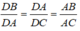
⇒ D A 2 = D B . D C
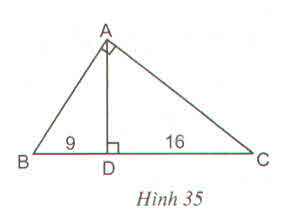
hay DA = D B . D C = 9 . 16 = 12 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ABD, ta có:
A B 2 = D A 2 + D B 2 = 9 2 + 12 2 = 225 ⇒ AB =15 (cm)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD,ta có:
AC2 = DA2 + DC2 = 122 +162 = 400 ⇒ AC = 20cm
Vậy BC = BD + DC = 9 + 16 = 25(cm)

A B C K H D E F
Ta giả sử AB < AC . Cần chứng minh AB + CH < AC + BK
Trên cạnh AC lấy điểm D sao cho AB = AD . Từ D lần lượt hạ các đường vuông góc với AB và AC lần lượt tại E và F.
Ta có tam giác ADE = tam giác ABK (đặc biệt) => DE = BK
Xét : \(AC+BK=AD+DC+CH=AB+CD+HF\)(Vì DEHF là hình chữ nhật => BK = DE = HF)
Mà trong tam giác vuông DFC có cạnh huyền CD nên ta có \(DC>CF\)
\(\Rightarrow AC+BK=AB+CD+HF>AB+CF+HF=AB+CH\)

a, Gọi AC giao BD tai O
TAm giác OAB có
OA + OB > AB (1)
Tam giác OCD có
OC + OD > CD (2)
cộng vế với vế của (1) và (2) -=> AC + BD > AB + CD

\(AB^2 + AC^2 = 25^2 = 625\)
\(AD^2 + 81 = AB^2\)
\(AD^2 + 256 = AC^2\)
\(=> AD^2 + 81 + AD^2 + 256 = 625\)
=> \(2AD^2 = 288\)
=> \(AD^2 = 144\)
=> AD = 12(cm)
=>\( AB^2 = 9^2 + 12^2 = 225\)
=> AB = 15 (cm)
=> \(AC^2 = 12^2 + 16^2 = 400\)
=> AC = 20(cm)
và BC = 25(cm)

Ta có: \(BC=BD+DC=9+16=25\left(cm\right)\)
Xét \(\Delta DBA\) và \(\Delta ABC\):
\(\widehat{A}=\widehat{D}\left(=90^o\right)\)
\(\widehat{B}=\widehat{A_2}\)(cùng phụ với góc\(A_1\))
\(\Rightarrow\Delta DBA\)~\(\Delta ABC\)
\(\Rightarrow\dfrac{DB}{AB}=\dfrac{AB}{BC}\Leftrightarrow AB^2=DB.BC=9.25=225\Rightarrow AB=15\left(cm\right)\)
Áp dụng định lý Py-ta-go cho tam giác vuông ABC, có:
\(AB^2+AC^2=BC^2\Leftrightarrow15^2+AC^2=25^2\Rightarrow AC=\sqrt{25^2-15^2}=20\)
Vậy các cạnh của tam giác vuông ABC lần lượt là: \(15;20;25\)
mk chauw học tham khảo câu hỏi tương tự nha bạn