Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Ta có:
O A ⊥ O C ( G T ) ⇒ A O C ^ = 90 ° O D ⊥ O B ( G T ) ⇒ D O B ^ = 90 ° A O D ^ + C O D ^ = A O C ^ = 90 ° B O C ^ + C O D ^ = D O B ^ = 90 °
⇒ A O D ^ = B O C ^ (Cùng phụ C O D ^ )
b. Ta có:
A O D ^ + B O D ^ = A O B ^ ⇒ A O D ^ + 90 ° = 130 ° ⇒ A O D ^ = 130 ° − 90 ° ⇒ A O D ^ = 40 °
Mà A O D ^ + C O D ^ = 90 ° ( C M T )
40 ° + C O D ^ = 90 ° C O D ^ = 50 °
c. OM là tia phân giác của A O B ^ nên:
A O M ^ = B O M ^ = A O B ^ 2 = 65 °
A O D ^ + D O M ^ = A O M ^ 40 ° + D O M ^ = 65 ° D O M ^ = 25 °
Tương tự ta tìm được C O M ^ = 25 °
Do đó C O M ^ = D O M ^ ( = 25 ° )
Vậy OM là tia phân giác của C O D ^

Ta có OC là tia phân giác AÔB => BÔC = AÔB/2 = 500/2 = 250
Ta có CÔD = BÔC + BÔD => BÔD = CÔD - BÔC = 900 - 250 = 650
Ta có OA đối OE => AÔE = 1800
Ta có AÔE = AÔB + BÔE => BÔE = AÔE - AÔB = 1800 - 500 = 1300
Ta có BÔE = BÔD + DÔE => DÔE = BÔE - BÔD = 1300 - 650 = 650
=> DÔE = DÔB ( = 650 ) mà tia OD nằm trong BÔE nên OD là tia phân giác của BÔE

Ta có OC là tia phân giác AOB => BOC = \(\frac{AOB}{2}\) = \(\frac{50^o}{2}\) = 250
Ta có COD = BOC + BOD => BOD = COD - BOC = 900 - 250 = 650
Ta có OA đối OE => AOE = 1800
Ta có AOE = AOB + BOE => BOE = AOE - AOB = 1800 - 500 = 1300
Lại có BOE = BOD + DOE => DOE = BOE - BOD = 1300 - 650 = 650
=> DOE = DOB ( = 650 ) mà tia OD nằm trong BOE nên OD là tia phân giác của BOE (đpcm)
Ta có OC là tia phân giác AOB => BOC = \(\frac{AOB}{2}\) = \(\frac{50^o}{2}\) = 250
Ta có COD = BOC + BOD => BOD = COD - BOC = 900 - 250 = 650
Ta có OA đối OE => AOE = 1800
Ta có AOE = AOB + BOE => BOE = AOE - AOB = 1800 - 500 = 1300
Lại có BOE = BOD + DOE => DOE = BOE - BOD = 1300 - 650 = 650
=> DOE = DOB ( = 650 ) mà tia OD nằm trong BOE nên OD là tia phân giác của BOE (đpcm)

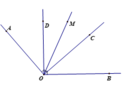
O A B D C M
a, Ta có
\(\widehat{AOD}=\widehat{AOB}-\widehat{BOD}\)
\(\Rightarrow\widehat{AOD}=130^0-90^0=40^0\) [ 1 ]
Mặt khác
\(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}\)
\(\Rightarrow\widehat{BOC}=130^0-90^0=40^0\) [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
\(\widehat{AOD}=\widehat{BOC}=40^0\)
b.Ta thấy
\(\widehat{AOB}=\widehat{AOD}+\widehat{COD}+\widehat{BOC}\)
\(\Rightarrow\widehat{COD}=\widehat{AOB}-2\widehat{AOD}\)[ vì góc AOD = góc BOC theo câu a ]
\(\Rightarrow\widehat{COD}=130^0-2.40^0\)
\(\Rightarrow\widehat{COD}=130^0-80^0=50^0\)
Vậy góc COD = 50độ
c.Vì OM là tia phân giác góc COD nên
\(\widehat{COM}=\widehat{DOM}=\frac{\widehat{COD}}{2}=\frac{50^0}{2}=25^0\)
Ta có
\(\widehat{AOM}=\widehat{AOD}+\widehat{DOM}\)
\(\Rightarrow\widehat{AOM}=40^0+25^0=65^0\)
mà \(\widehat{BOM}=\widehat{BOC}+\widehat{COM}\)
\(\Rightarrow\widehat{BOM}=40^0+25^0=65^0\)
Suy ra \(\widehat{AOM}=\widehat{BOM}\)
Vậy OM là tia phân giác góc AOB
Chúc bạn học tốt

Làm ơn giúp mình với, mai mình phải nộp rồi ![]()
Bạn nào trả lời nhanh mình tick cho! ![]()