Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a. Ta có:
O A ⊥ O C ( G T ) ⇒ A O C ^ = 90 ° O D ⊥ O B ( G T ) ⇒ D O B ^ = 90 ° A O D ^ + C O D ^ = A O C ^ = 90 ° B O C ^ + C O D ^ = D O B ^ = 90 °
⇒ A O D ^ = B O C ^ (Cùng phụ C O D ^ )
b. Ta có:
A O D ^ + B O D ^ = A O B ^ ⇒ A O D ^ + 90 ° = 130 ° ⇒ A O D ^ = 130 ° − 90 ° ⇒ A O D ^ = 40 °
Mà A O D ^ + C O D ^ = 90 ° ( C M T )
40 ° + C O D ^ = 90 ° C O D ^ = 50 °
c. OM là tia phân giác của A O B ^ nên:
A O M ^ = B O M ^ = A O B ^ 2 = 65 °
A O D ^ + D O M ^ = A O M ^ 40 ° + D O M ^ = 65 ° D O M ^ = 25 °
Tương tự ta tìm được C O M ^ = 25 °
Do đó C O M ^ = D O M ^ ( = 25 ° )
Vậy OM là tia phân giác của C O D ^

Làm ơn giúp mình với, mai mình phải nộp rồi ![]()
Bạn nào trả lời nhanh mình tick cho! ![]()

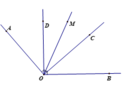
O A B D C M
a, Ta có
\(\widehat{AOD}=\widehat{AOB}-\widehat{BOD}\)
\(\Rightarrow\widehat{AOD}=130^0-90^0=40^0\) [ 1 ]
Mặt khác
\(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}\)
\(\Rightarrow\widehat{BOC}=130^0-90^0=40^0\) [ 2 ]
Từ [ 1 ] và [ 2 ] suy ra
\(\widehat{AOD}=\widehat{BOC}=40^0\)
b.Ta thấy
\(\widehat{AOB}=\widehat{AOD}+\widehat{COD}+\widehat{BOC}\)
\(\Rightarrow\widehat{COD}=\widehat{AOB}-2\widehat{AOD}\)[ vì góc AOD = góc BOC theo câu a ]
\(\Rightarrow\widehat{COD}=130^0-2.40^0\)
\(\Rightarrow\widehat{COD}=130^0-80^0=50^0\)
Vậy góc COD = 50độ
c.Vì OM là tia phân giác góc COD nên
\(\widehat{COM}=\widehat{DOM}=\frac{\widehat{COD}}{2}=\frac{50^0}{2}=25^0\)
Ta có
\(\widehat{AOM}=\widehat{AOD}+\widehat{DOM}\)
\(\Rightarrow\widehat{AOM}=40^0+25^0=65^0\)
mà \(\widehat{BOM}=\widehat{BOC}+\widehat{COM}\)
\(\Rightarrow\widehat{BOM}=40^0+25^0=65^0\)
Suy ra \(\widehat{AOM}=\widehat{BOM}\)
Vậy OM là tia phân giác góc AOB
Chúc bạn học tốt

Bài 2: ta có: góc AOC+góc AOD=180 độ(vì kề bù) mà góc AOC-AOD= 20 độ => AOC= (180+20):2= 100độ
=> AOD= 100- 20= 80độ
ta có: COB = AOD( vì đối đỉnh)=> COB=80độ
BOD=AOC (vì đối đỉnh)=> BOD=100độ