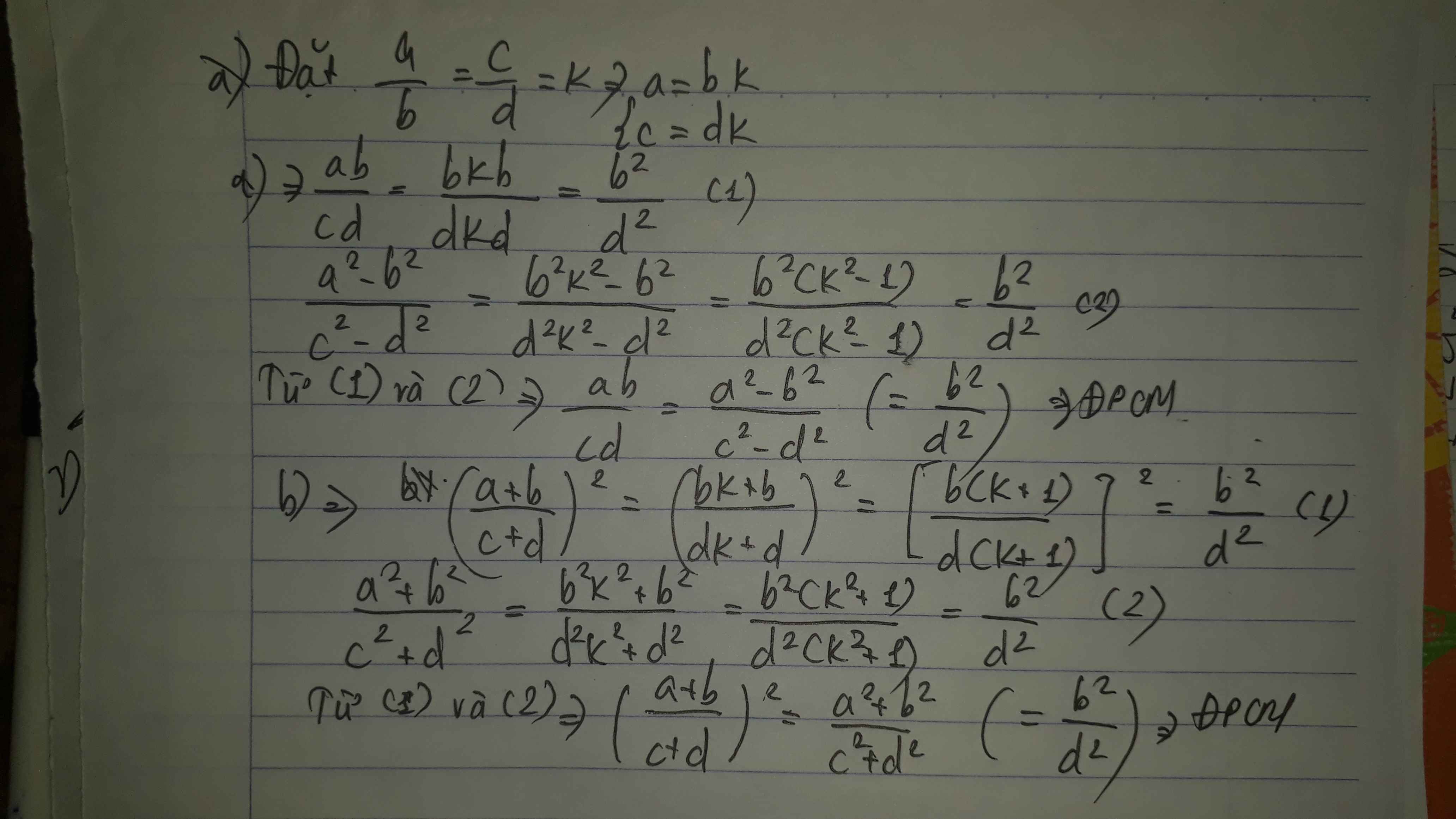Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)\(\frac{ab}{cd}=\frac{bk.b}{dk.b}=\frac{b^2}{d^2}\left(1\right)\)
\(\frac{a^2-b^2}{c^2-d^2}=\frac{b^2k^2-b^2}{d^2k^2-d^2}=\frac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\frac{b^2}{d^2}\left(2\right)\)
từ\(\left(1\right)\)và\(\left(2\right)\)\(\Rightarrow\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)

\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)(tc dãy tỉ số bằng nhau)
\(\Rightarrow\frac{a}{b}\cdot\frac{c}{d}=\frac{a+c}{b+d}\cdot\frac{a+c}{b+d}\Rightarrow\frac{ac}{bd}=\frac{\left(a+c\right)^2}{\left(b+d\right)^2}\)

Ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{a+b}{c+d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\left(\frac{a+b}{c+d}\right)^2\left(1\right)\)
\(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2+b^2}{c^2+d^2}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\left(\frac{a+b}{c+d}\right)^2=\frac{a^2+b^2}{c^2+d^2}\left(đpcm\right)\)
đặt a/b = c/d = k (k thuộc N)
=> a = bk
c = dk
thay a và c vào 2 phân số cần so sánh thì = nhau

\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a^{1994}}{b^{1994}}=\frac{c^{1994}}{d^{1994}}\)
áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\frac{a^{1994}}{b^{1994}}=\frac{\left(a+c\right)^{1994}}{\left(b+d\right)^{1994}}\)(1)
\(\frac{a^{1994}}{b^{1994}}=\frac{c^{1994}}{d^{1994}}=\frac{a^{1994}+c^{1994}}{b^{1994}+d^{1994}}\)(2)
từ (1) và (2) => \(\frac{a^{1994}+c^{1994}}{b^{1994}+d^{1994}}=\frac{\left(a+c\right)^{1994}}{\left(b+d\right)^{1994}}\left(đpcm\right)\)
\(\)

Nguyễn Thị Linh Chi: Em có cách khác ạ. (cách này em làm trên lớp thường ngày.Và cũng khác đơn giản ạ)
ĐK: b,d ≠ 0 ; b≠d
Ta có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\).Đặt \(\frac{a}{c}=\frac{b}{d}=k\Rightarrow\hept{\begin{cases}a=kc\\b=kd\end{cases}}\).Thay vào:
\(\frac{\left(a+b\right)^2}{a^2+b^2}=\frac{\left(kc+kd\right)^2}{k^2c^2+k^2d^2}=\frac{\left[k\left(c+d\right)\right]^2}{k^2\left(c^2+d^2\right)}=\frac{\left(c+d\right)^2}{c^2+d^2}^{\left(đpcm\right)}\)

\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a^6}{b^6}=\frac{c^6}{d^6}=\frac{3a^6}{3b^6}\)
áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{a^6}{b^6}=\frac{c^6}{d^6}=\frac{3a^6}{3b^6}=\frac{3a^6+c^6}{3b^6+d^6}\left(1\right)\)
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow\frac{a^6}{b^6}=\frac{c^6}{d^6}=\frac{\left(a+c\right)^6}{\left(b+d\right)^6}\left(2\right)\)
từ (1) và (2) => đpcm