Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chứng minh rằng nếu tứ giác ABCD có hai đường chéo vuông góc với nhau thì tổng bình phương hai cạnh đối này bằng tổng bình phương hi cạnh đối kia.
Gọi giao của AC và BD là O , do hai đường chéo vuông góc
=> các tam giác : OAB, OBC, OCD, ODA là các tam giác vuông tại O
xét tam giác OAB có AB^2 = OA^2 + OB^2 (1)
xét tam giác ODC có DC^2 = OD^2 + OC^2 (2)
xét tam giác OAD có AD^2 = OA^2 + OD^2 (3)
xét tam giác OBC có BC^2 = OC^2 + OB^2 (4)
từ (1) và (2)=> AB^2 + CD^2 = OA^2 +OB^2 +OC^2 +OD^2 (5)
từ (3) và (4)=> BC^2 + AD^2 = OA^2 +OB^2 +OC^2 +OD^2 (6)
từ (5) và (6) => AB^2 + CD^2 = BC^2 + AD^2 (điều phải c/m )
Tam giác AID vuông tại I, áp dụng định lí Pytago, ta có A{D^2} = A{I^2} + I{D^2} (1)
Tam giác AID vuông tại I, áp dụng định lí Pytago, ta có A{B^2} = A{I^2} + I{B^2} (2)
Tam giác AID vuông tại I, áp dụng định lí Pytago, ta có C{D^2} = C{I^2} + I{D^2} (3)
Tam giác AID vuông tại I, áp dụng định lí Pytago, ta có B{C^2} = B{I^2} + I{C^2} (4)
Vế cộng vế (1) và (4), ta được: A{D^2} + B{C^2} = 2\left( {I{A^2} + I{B^2} + I{C^2} + I{D^2}} \right) (5)
Vế cộng vế (2) và (3), ta được: A{B^2} + C{D^2} = 2\left( {I{A^2} + I{B^2} + I{C^2} + I{D^2}} \right) (6)
Từ (5) và (6), ta suy ra A{D^2} + B{C^2} = A{B^2} + C{D^2} (đpcm)

A B C D M E F
a) Do AD // FM nên \(\widehat{BAD}=\widehat{AFE}\) (Hai góc đồng vị)
Cũng do AD // FM nên \(\widehat{DAC}=\widehat{AEF}\) (Hai góc so le trong)
AD là phân giác nên \(\widehat{BAD}=\widehat{DAC}\)
Vậy nên \(\widehat{AEF}=\widehat{AFE}\)
b) Ta thấy \(\widehat{MEC}=\widehat{AEF}\) (Hai góc đối đỉnh)
Mà \(\widehat{AEF}=\widehat{AFE}\) (cma)
Vậy nên \(\widehat{MEC}=\widehat{AFE}\).

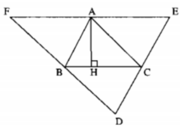
a: Xét tứ giác BFED có
ED//BF
FE//BD
Do đó: BFED là hình bình hành
Xét ΔABC có
D là trung điểm của BC
DE//AB
Do đó: E là trung điểm của AC
Xét ΔABC có
E là trung điểm của AC
EF//CB
Do đó: F là trung điểm của AB
Xét ΔCDE và ΔEFA có
CD=EF
DE=FA
CE=EA
Do đó: ΔCDE=ΔEFA
b: Gọi ΔABC có F là trung điểm của AB,E là trung điểm của AC
Trên tia FE lấy điểm E sao cho E là trung điểm của FK
Xét tứ giác AFCK có
E là trung điểm của AC
E là trung điểm của FK
Do đó: AFCK là hình bình hành
Suy ra: AF//KC và KC=AF
hay KC//FB và KC=FB
Xét tứ giác BFKC có
KC//FB
KC=FB
Do đó: BFKC là hình bình hành
Suy ra: FE//BC(ĐPCM)

\(\frac{3x-y}{x+y}=\frac{3}{4}\)
\(\Leftrightarrow4\left(3x-y\right)=3\left(x+y\right)\)
\(\Leftrightarrow12x-4y=3x+3y\)
\(\Leftrightarrow12x-4y-3x-3y=0\)
\(\Leftrightarrow9x-7y=0\)
\(\Leftrightarrow9x=7y\Leftrightarrow\frac{x}{7}=\frac{y}{9}\)

Xét ΔABC và ΔCEA, ta có:
∠(ACB) = ∠(CAE) (so le trong, AE // BC)
AC cạnh chung
∠(CAB) = ∠(ACE) (so le trong, CE // AB)
Suy ra: ΔABC = ΔCEA (g.c.g)
⇒ BC = AE (1)
Xét ΔABC và ΔBAF, ta có:
∠(ABC) = ∠(BAF) (so le trong, AF // BC)
AB cạnh chung
∠(BAC) = ∠(ABF) (so le trong, BF // AC)
Suy ra: ΔABC = ΔBAF (g.c.g)
⇒ AF = BC (2)
Từ (1) và (2) suy ra: AE = AF
Vậy A là trung điểm của EF.