Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\frac{a}{b}< \frac{c}{d}\)
\(\Rightarrow ad< bc\)
\(\Rightarrow ab+ad< bc+ab\)
\(\Rightarrow a\left(b+d\right)< b\left(a+c\right)\)
\(\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}\)( 1 )
Lại có : ad < bc
\(\Rightarrow ad+cd< bc+cd\)
\(\Rightarrow d\left(a+c\right)< c\left(b+d\right)\)
\(\Rightarrow\frac{a+c}{b+d}< \frac{c}{d}\)( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
Ta có : \(\frac{a}{b}<\frac{c}{d}\Rightarrow\frac{ad}{bd}<\frac{cb}{bd}\)
\(\Rightarrow\)\(ad\)\(<\)\(cb\) (vì \(bd>0\)) \(\left(1\right)\)
\(\frac{a}{b}=\frac{a\left(b+d\right)}{b\left(b+d\right)}=\frac{ab+ad}{b\left(b+d\right)}\)
\(\frac{a+c}{b+d}=\frac{\left(a+c\right)b}{\left(b+d\right)b}=\frac{ab+cb}{b\left(b+d\right)}\)
vì \(b,d>0\Rightarrow b\left(b+d\right)>0\) \(\left(1\right)\)
vì \(ad\)\(<\)\(cd\Rightarrow\)\(ab+ad\)\(<\)\(ab+cb\) \(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\) \(\frac{ab+ad}{b\left(b+d\right)}<\frac{ab+cb}{b\left(b+d\right)}\)
hay \(\frac{a}{b}<\frac{a+c}{b+d}\) \(\left(\cdot\right)\)
\(\frac{a+c}{b+d}=\frac{d\left(a+c\right)}{d\left(b+d\right)}=\frac{ad+cd}{d\left(b+d\right)}\)
\(\frac{c}{d}=\frac{c\left(b+d\right)}{d\left(b+d\right)}=\frac{cb+cd}{d\left(b+d\right)}\)
Vì \(ad\)\(<\)\(cd\Rightarrow\)\(ad+cd<\)\(cb+cd\) \(\left(3\right)\)
Từ \(\left(1\right)\) và \(\left(3\right)\) \(\Rightarrow\frac{ad+cd}{d\left(b+d\right)}<\frac{cb+cd}{d\left(b+d\right)}\)
hay \(\frac{a+c}{b+d}<\frac{c}{d}\) \(\left(\cdot\cdot\right)\)
Từ \(\left(\cdot\right)\) và \(\left(\cdot\cdot\right)\Rightarrow\frac{a}{b}<\frac{a+c}{b+d}<\frac{c}{d}\)
Ta có:a/b<c/d =>ad<bc (1)
Thêm ab vào (1) ta đc:
ad+ab<bc+ab hay a(b+d)<b(a+c) =>a/b<a+c/b+d (2)
Thêm cd vào 2 vế của (1), ta lại có:
ad+cd<bc+cd hay d(a+c)<c(b+d) => c/d>a+c/b+d (3)
Từ (2) và (3) suy ra:a/b<a+c/b+d<c/d
ta có:a/b<c/d nên ad<bc
(1)ab+ad<ab+bc=a(b+d)<b(a+c)=>a/b<a+c/b+d(thêm ab vào hai vế)
(2)ad+cd<bc+cd=(a+c)d<(b+d)c=>a+c/b+d<c/d(thêm cd vào hai vế)
từ(1)và(2)ta có:a/b<a+c/b+d<c/d
Bạn tham khảo tại đây:
Câu hỏi của Mạnh Khuất - Toán lớp 7 - Học toán với OnlineMath
\(\frac{a}{b}< \frac{c}{d}\Rightarrow ad< bc\)
+) \(ad+ab< bc+ab\Leftrightarrow a\left(b+d\right)< b\left(a+c\right)\Leftrightarrow\frac{a}{b}< \frac{a+c}{b+d}\)( 1 )
+) \(ad+cd< bc+cd\Leftrightarrow d\left(a+c\right)< c\left(b+d\right)\Leftrightarrow\frac{a+c}{b+d}< \frac{c}{d}\)( 2 )
Từ ( 1 ) và ( 2 ) \(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
Ta có: \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow\frac{ad}{bd}< \frac{bc}{bd}\)
Vì \(b,d>0\Rightarrow bd>0\)
\(\Rightarrow ad< bc\)
Ta lại có:
\(\frac{a}{b}=\frac{a\left(b+d\right)}{b\left(b+d\right)}=\frac{ab+ad}{b\left(b+d\right)}\)
\(\frac{a+c}{b+d}=\frac{b\left(a+c\right)}{b\left(b+d\right)}=\frac{ab+bc}{b\left(b+d\right)}\)
Vì \(b,d>0\)
Nên \(b\left(b+d\right)>0\)và \(d\left(b+d\right)>0\) \(\left(1\right)\)
Mà \(ad< bc\Leftrightarrow ab+ad< ab+bc\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)ta có: \(\frac{ab+ad}{b\left(b+d\right)}>\frac{ab+bc}{b\left(b+d\right)}\)
\(\Rightarrow\frac{a}{b}< \frac{a+c}{b+d}\left(\cdot\right)\)
Ta lại có:
\(\frac{a+c}{b+d}=\frac{d\left(a+c\right)}{d\left(b+d\right)}=\frac{ad+cd}{d\left(b+d\right)}\)
\(\frac{c}{d}=\frac{c\left(b+d\right)}{d\left(b+d\right)}=\frac{bc+cd}{d\left(b+d\right)}\)
Mà \(ad< bc\Rightarrow ad+cd< bc+cd\left(3\right)\)
Từ \(\left(1\right)\)và \(\left(3\right)\)ta có:
\(\frac{ad+cd}{d\left(b+d\right)}< \frac{bc+cd}{d\left(b+d\right)}\)
\(\Rightarrow\frac{a+c}{b+d}< \frac{c}{d}\left(\cdot\cdot\right)\)
Từ \(\left(\cdot\right)\)và \(\left(\cdot\cdot\right)\)ta có: \(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
Vì \(\frac{a}{b}\) < \(\frac{c}{d}\) nên ad < bc (1)
Xét tích a(b + d) = ab + ad (2)
b ( a + c ) = ba + bc (3)
Từ (1);(2);(3) suy ra a(b+d) < b(a+c) do đó \(\frac{a}{b}\) < \(\frac{a+c}{b+d}\) (4)
Tương tự ta có \(\frac{a+c}{b+d}\) < \(\frac{c}{d}\) (5)
kết hợp (4) ; (5) ta được \(\frac{a}{b}\) < \(\frac{a+c}{b+d}\) < \(\frac{c}{d}\)
vì \(\frac{a}{b}< \frac{c}{d}=>ad< bc\)
=>ad+ab<bc+ab
=>a(b+d)<b(a+c)
=>\(\frac{a}{b}< \frac{a+c}{b+d}\) (1)
vì \(\frac{a}{b}< \frac{c}{d}=>ad< bc\)
=>ad+cd<bc+cd
=>a(a+c)<c(b+d)
=>\(\frac{a+c}{b+d}< \frac{c}{d}\) (2)
từ (1)(2)=>\(\frac{a}{b}< \frac{a+c}{b+d}< \frac{c}{d}\)
chúc bạn học tốt
Áp dụng kết quả bài 5, ta có: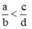
⇒ ad < bc (1)
Cộng cả hai vế của (1) với ab ta có: ab + ad < ab + bc
hay a(b + d) < b.(a + c)
Cộng cả hai vế của (1) với cd ta có: ad + cd < bc + cd
Hay d(a + c) < c(b + d)
Vậy