Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
A={0;1;2;3;4;5;6;7;8;9}
Các tập con có A có hai phần tử mà có chứa chữ số 0 là:
{0;1},{0;2},{0;3},{0;4},{0;5},{0;6},{0;7},{0;8},{0;9}
Vậy có 9 tập con thỏa mãn bài toán.

a, Sơ đồ tư duy:
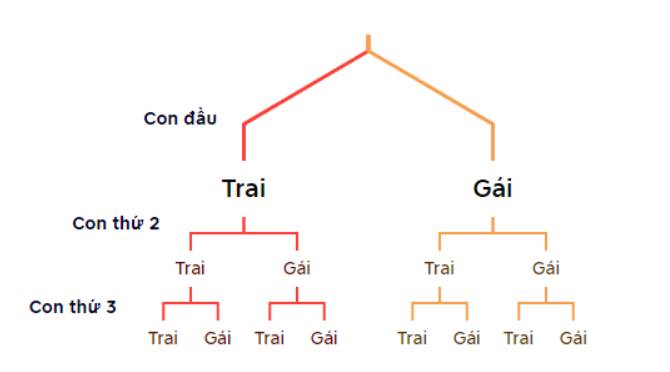
Kí hiệu con trai: T, con gái: G.
Các kết quả có thể xảy ra là: GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT.
Do đó: \(\Omega\)= {GGG; GGT; GTG; GTT; TGG; TGT; TTG; TTT}.
Vậy n(Ω) = 8.
b) Gọi biến cố A: “Gia đình đó có một con trai và hai con gái”.
Ta có: A = {GTG; TGG; GGT}. Do đó, \(n(A)\)= 3.
Vậy \(P(A) = \frac{{n(A)}}{{n(\Omega )}} = \frac{3}{8}\)

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 3 của 4 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_4^3\) ( phần tử)
b) +) Sự kiện “Tổng các số trên ba tấm bìa bằng 9” tương ứng với biến cố \(A = \left\{ {\left( {4;3;2} \right)} \right\}\)
+) Sự kiện “Các số trên ba tấm bìa là ba số tự nhiên liên tiếp” tương ứng với biến cố \(B = \left\{ {\left( {1;2;3} \right),\left( {2;3;4} \right)} \right\}\)
c) +) Ta có: \(n\left( A \right) = 1\),\(n\left( B \right) = 2\)
+) Vậy xác suất của biến cố A và B là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{4};P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{2}{4} = \frac{1}{2}\)

a) Mỗi phần tử của không gian mẫu là một tổ hợp chập 2 của 5 phần tử. Do đó, số phần tử của không gian mẫu là: \(n\left( \Omega \right) = C_5^2\) ( phần tử)
b)
+) Gọi A là biến cố “Tích các số trên hai thẻ là số lẻ”
+) Để tích các số trên thẻ là số lẻ thì cả hai thẻ bốc được đểu phải là số lẻ. Do đó, số phần tử các kết quả thuận lợi cho biến cố A là tổ hợp chập 2 của 3 phần tử: \(n\left( A \right) = C_3^2\) ( phần tử)
+) Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{{C_3^2}}{{C_5^2}} = \frac{3}{{10}}\)