Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

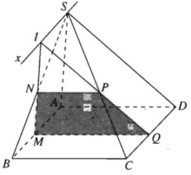
a) Vì M ∈ (SAB)
Và 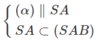 nên (α) ∩ (SAB) = MN
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và 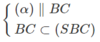 nên (α) ∩ (SBC) = NP
nên (α) ∩ (SBC) = NP
và NP // BC (1)
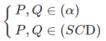 ⇒ (α) ∩ (SCD) = PQ
⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và 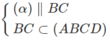 nên (α) ∩ (ABCD) = QM
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
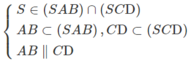 ⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒ 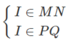
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.

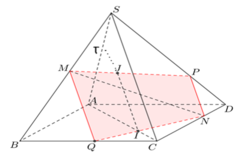
+) Qua N kẻ NP// SC .
- Ta có: 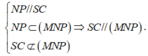
- Từ đó ta có: (MNP) là mặt phẳng qua MN và song song với SC.
- Vậy (P) ≡ (MNP).
+) Ta có: (P) ∩ (SCD) = NP.
- Ta có: 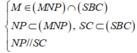
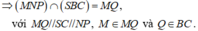
+) Trong (ABCD), gọi I = NQ ∩ AC.
- Ta có: 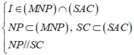
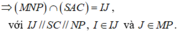

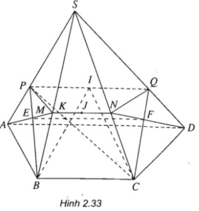
a) Ta có: I ∈ (SAD) ⇒ I ∈ (SAD) ∩ (IBC)
Vậy
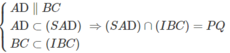
Và PQ //AD // BC (1)
Tương tự: J ∈ (SBC) ⇒ J ∈ (SBC) ∩ (JAD)
Vậy
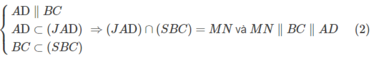
Từ (1) và (2) suy ra PQ // MN.
b) Ta có:
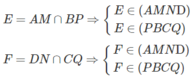
Do đó: EF = (AMND) ∩ (PBCQ)
Mà
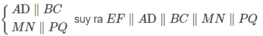
Tính
EF: CP ∩ EF = K ⇒ EF = EK + KF
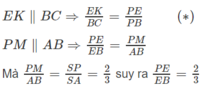
Từ (∗) suy ra
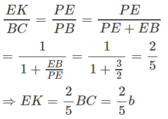
Tương tự ta tính được KF = 2a/5
Vậy: 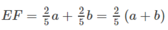
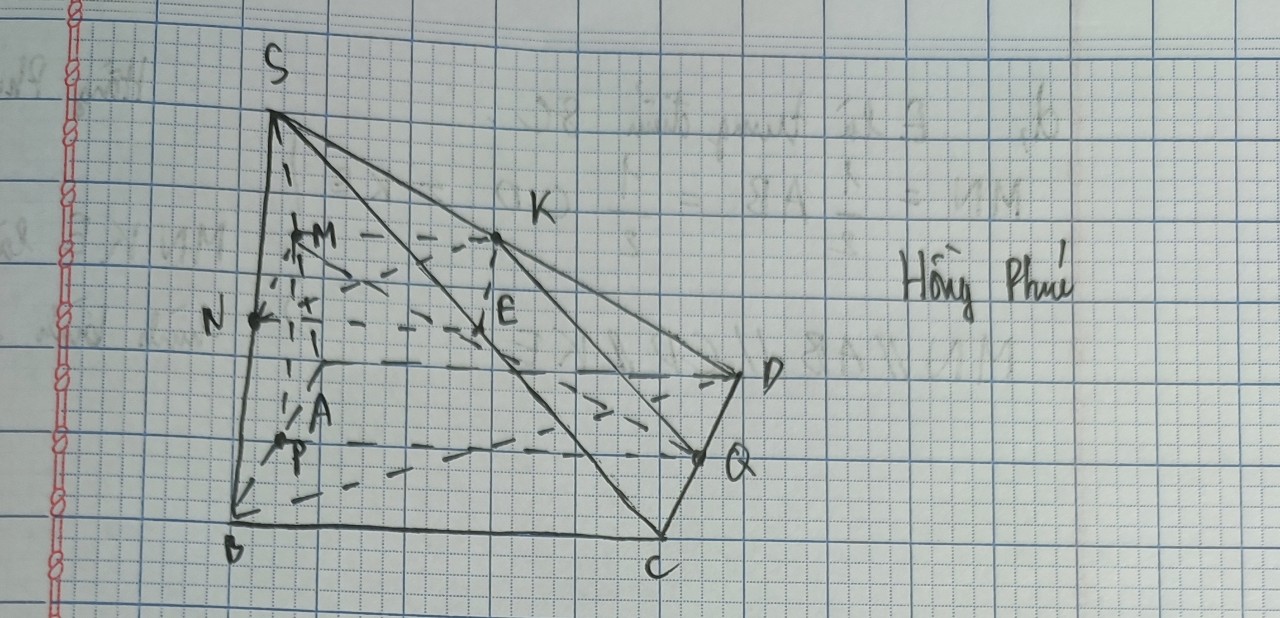
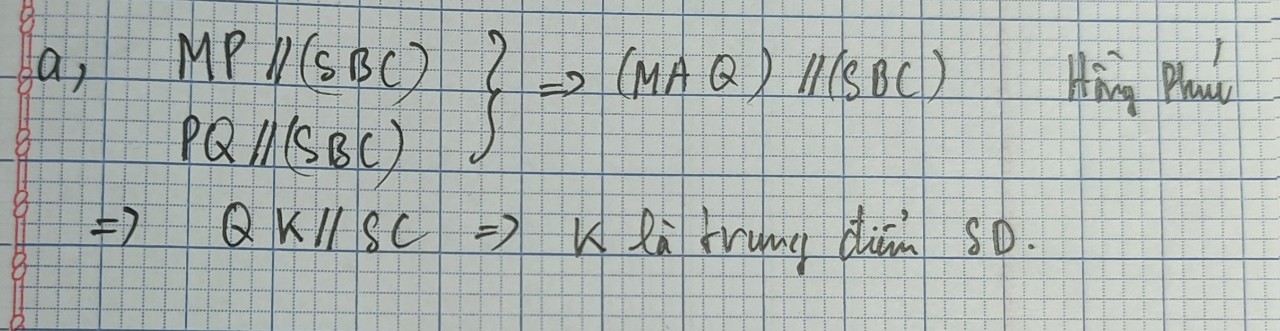


a: Ta có: MQ//CD
CD//AB
Do đó: MQ//AB
mà MQ⊂(MNPQ)
nên AB//(MNPQ)
Ta có: MN//SB
=>SB//(MNPQ)
Ta có: AB//(MNPQ)
SB//(MNPQ)
AB cắt SB tại B
AB,SB cùng thuộc mp(SAB)
Do đó: (SAB)//(MNPQ)
mà (MNPQ) cắt (SAD)=PQ
và (SAB) cắt (SAD)=SA
nên PQ//SA