Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi K=AM∩SOK=AM∩SO. Mặt phẳng (P) đi qua K và song song với BD nên cắt (SBD) theo giao tuyế d' đi qua K và song song với BD. Vậy qua K, ta vẽ d' song song với BD. Đường thẳng d' cắt SB và SD lần lượt tại E và F. Đây là các điểm cần tìm.
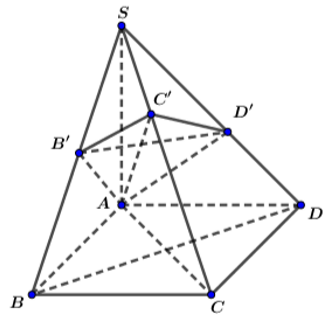
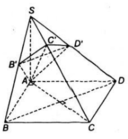
Mặt phẳng (P) qua A song song với BD nên (P) sẽ cắt (ABCD) theo giao tuyến d đi qua A và song song với BD. A và BD cố định nên d cố đinh
Đáp án C
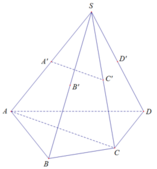
Mặt phẳng (P) đi qua A’ và song song AC
Trong mặt phẳng (SAC), ta có A’C’//AC (A’C’ là đường trung bình tam giác SAC)
⇒ (P) đi qua A’C’ cố định
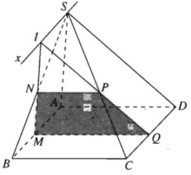
a) Vì M ∈ (SAB)
Và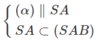 
nên (α) ∩ (SAB) = MN
và MN // SA
Vì N ∈ (SBC)
Và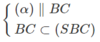 
nên (α) ∩ (SBC) = NP
và NP // BC (1)
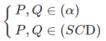⇒ (α) ∩ (SCD) = PQ
Q ∈ CD ⇒ Q ∈ (ABCD)
Và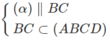 
nên (α) ∩ (ABCD) = QM
và QM // BC (2)
Từ (1) và (2) suy ra tứ giác MNPQ là hình thang.
b) Ta có:
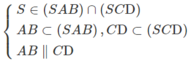⇒ (SAB) ∩ (SCD) = Sx và Sx // AB // CD
MN ∩ PQ = I ⇒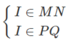 
MN ⊂ (SAB) ⇒ I ∈ (SAB), PQ ⊂ (SCD) ⇒ I ∈ (SCD)
⇒ I ∈ (SAB) ∩ (SCD) ⇒ I ∈ Sx
(SAB) và (SCD) cố định ⇒ Sx cố định ⇒ I thuộc Sx cố định.
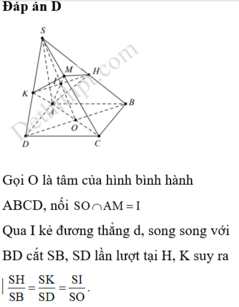
Đáp án D
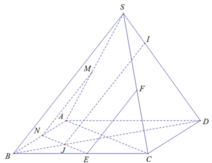
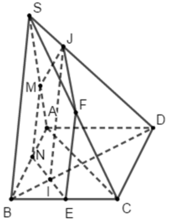
Gọi M là điểm bất kì trên cạnh SA
Trong (SAB), kẻ Mx // SB, Mx cắt AB tại N
Trong (ABCD), kẻ Ny // AC, Ny cắt BC tại E
Ny cắt BD tại J
Trong (SBC), kẻ Ez // SB, Ez cắt SC tại F
Trong (SBD), kẻ Jt // SB, Jt cắt SD tại I
⇒ IJ // (SAB)
