K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 5 2022
a: XétΔABC có
AD là đường cao
BE là đường cao
AD cắt BE tại H
Do đó: CH⊥AB
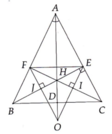
b: Ta có: ΔFBC vuông tại F
mà FD là trung tuyến
nên FD=BC/2(1)
Ta có: ΔEBC vuông tại E
mà ED là trung tuyến
nên ED=BC/2(2)
Từ (1) và (2) suy ra FD=ED(3)
Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
AB=AC
góc A chung
Do đó: ΔAEB=ΔAFC
SUy ra: AE=AF(4)
Từ (3) và (4) suy ra AD là đường trung trực của EF
10 tháng 5 2022
a: Xét tứ giác BGCH có
M là trung điểm của GH
M là trung điểm của BC
Do đó; BGCH là hình bình hành
SUy ra: BG//CH
b: Xét ΔBMK vuông tại M và ΔCMJ vuông tại M có
MB=MC
\(\widehat{MBK}=\widehat{MCJ}\)
Do đó: ΔBMK=ΔCMJ
Suy ra: BK=CJ
I
5 tháng 1 2023
a, Tam giác \(ABC\) cân tại \(A\)
\(\Rightarrow AB=AC;\widehat{B}=\widehat{C}\)
Xét \(\Delta ABM;\Delta ACM\) có
\(AB=AC\left(cmt\right)\\ \widehat{B}=\widehat{C}\left(cmt\right)\\ MB=MC\)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c-g-c\right)\)
b, \(\Delta ABM=\Delta ACM\left(cmt\right)\)
\(\Rightarrow\widehat{HAM}=\widehat{KAM}\)
Xét \(\Delta AHM;\Delta AKM\) có
\(\widehat{HAM}=\widehat{KAM}\left(cmt\right)\\ \widehat{AHM}=\widehat{AKM}=90^o\)
\(AM\) chung
\(\Rightarrow\Delta AHM=\Delta AKM\left(ch-gn\right)\)
\(\Rightarrow HM=KM\)
LN
1
6 tháng 12 2015
76+75-74=74.72+74.7-74=74.(72+7-1)=74.55=74.5.11 chia hết cho 11
Vậy 76+75-74 chia hết cho 11
16 tháng 6 2021
gọi giao điểm của AJ với BD là H
giao điểm của AI với BD là E
giao điểm 2 đường chéo AC và BD là K
do ABCD là hình bình hành\(=>\left\{{}\begin{matrix}AK=KC\\KD=KB\end{matrix}\right.\)
\(=>DK\) là tiếp tuyến trong \(\Delta ADC\)
mà AJ cũng là tiếp tuyến trong \(\Delta ADC\)(do J là trung điểm CD)
\(=>H\) là trọng tâm \(=>BH=\dfrac{2}{3}DK=\dfrac{2}{3}.\dfrac{1}{2}.BD=\dfrac{1}{3}BD\left(1\right)\)
chứng minh tương tự đối với \(\Delta ACB=>E\) là trọng tâm
\(=>BE=\dfrac{2}{3}KB=\dfrac{2}{3}.\dfrac{1}{2}.BD=\dfrac{1}{3}BD\left(2\right)\)
\(\left(1\right)\left(2\right)\)\(=>HE=\dfrac{1}{3}BD=HD=EB\left(dpcm\right)\)
Sử dụng phương pháp phản chứng là đi tìm sự mâu thuẫn từ giả thuyết đến kết luận, tức là nếu ta muốn chứng minh kết luận của bài toán là đúng thì phải chúng minh cái ngược lại với nó là sai[1].
??????????????