Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Nếu A, B, C không thẳng hàng thì 3 điểm A, B, C tạo thành 3 đỉnh của 1 tam giác.
Trong tam giác ABC ta có AB + AC > BC
- Nếu A, B, C thẳng hàng và A ở giữa B và C hoặc trùng B, C thì AB + AC = BC
• Nếu A nằm giữa B và C thì AB + AC = BC.
• Nếu B nằm giữa A và C thì AB + BC = AC nên AC > BC.
Suy ra: AC + AB > BC
• Nếu C nằm giữa A và B thì AC + CB = AB nên AB > BC.
Suy ra: AB + AC > BC.
Vậy với ba điểm A, B, C bất kỳ ta luôn có AB + AC ≥ BC

Sửa đề: AB>=AC
Ta có: \(\widehat{AMB}+\widehat{AMC}=180^0\)
nên \(\left[{}\begin{matrix}\widehat{AMB}>90^0\\\widehat{AMC}>=90^0\end{matrix}\right.\)
Nếu \(\widehat{AMC}>=90^0\) thì ΔAMC có cạnh AC là cạnh lớn nhất
nên AC>AM
Nếu \(\widehat{AMB}>90^0\) thì ΔABM có AB là cạnh lớn nhất
=>AB>AM
mà AB<AC
nên AM<AC

A B C D
Trên tia đối của tia AB lấy D sao cho AD = AC
Do tia CA nằm giữa hai tia CB và CD nên
\(\widehat{BCD}>\widehat{ACD}\) (1)
Mặt khác, theo cách dựng, tam giác ACD cân tại A nên
\(\widehat{ACD}=\widehat{ADC}=\widehat{BDC}\) (2)
Từ (1) và (2) suy ra :
\(\widehat{BCD}>\widehat{BDC}\)
\(\Rightarrow BD>BC\) (quan hệ góc và cạnh đối diện trong \(\Delta BCD\))
\(\Rightarrow AB+AC>BC\)
Chỉ khi \(A,B,C\) thẳng hàng
\(\Rightarrow AB+AC=BC\)

a) ∆ABC có cạnh BC lớn nhất nên chân đường cao kẻ từ A phải nằm giữa B và C
=> HB + HC = BC
∆AHC vuông tại H => HC < AC
∆AHB vuông tại H => HB < AB
Cộng theo vế hai bất đẳng thức ta có:
HB + HC < AC + AB
Hay BC < AC + AB
b) BC là cạnh lớn nhất nên suy ra AB < BC và AC < BC
Do đó AB < BC + AC; AC < BC +AB
(cộng thêm AC hoặc AB vào vế phải của bất đẳng thức)

Hình tự vẽ nha bạn
a)Xét tam giác ABM và tam giác CEM có:
BM=MC(gt)
\(\widehat{AMB}=\widehat{CME}\)(2 góc đối đỉnh)
AM=ME(gt)
\(\Rightarrow\)tam giác AMB=tam giác CME(c-g-c)
=> AB=CE(2 cạnh tương ứng)
Vì M là trung điểm của AE \(\Rightarrow AM=\frac{1}{2}AE\)
b) Bất đẳng thức đối với tam giác ACE là: AC+CE>AE
CE - AC < AE
Vì AB=CE(theo chứng minh trên) => AC+AB>AE \(\Rightarrow\frac{AC+AB}{2}>\frac{AE}{2}=AM\)(1)
AB - AC < AE \(\Rightarrow\frac{AB-AC}{2}< \frac{AE}{2}=AM\)(2)
Từ (1) và (2) \(\Rightarrow\frac{AB-AC}{2}< AM< \frac{AB+AC}{2}\)

ta có:\(\left(\sqrt{a}-\sqrt{b}\right)\ge0\)
\(\Rightarrow a-2\sqrt{ab}+b\ge0\)
\(\Rightarrow a+b\ge2\sqrt{ab}\)
\(\Rightarrow\frac{a+b}{2}\ge\sqrt{ab}\)
dấu "=" xảy ra khi a=b
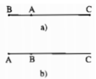
Xét 2 trường hợp:
+ A, B, C thẳng hàng và A nằm giữa B và C:
Khi đó AB + AC = BC
+ A, B, C không thẳng hàng hay A, B, C thẳng hàng nhưng A không nằm giữa B và C:
Khi đó AB + AC > BC
Vậy \(AB+AC\ge BC\)