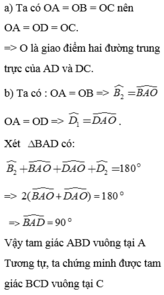Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

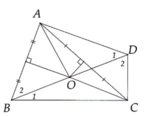
a, Xet tam giac AOB va tam giac COD co:
OA = OC (O la trung diem AC)
OB = OD (gt)
goc BOA = goc DOC (doi dinh)
suy ra tam giac BOA = tam giac DOC (c.g.c)
suy ra canh AB = canh CD (1), goc BAC = goc ODC (2)
b, xet tam giac ABC va tam giac CDA co:
AB = CD
goc BAC = goc ACD
AC chung
suy ra tam giac ABC = tam giac CDA (c.g.c)
suy ra BC = AD
c, xet tam giac ABD va tam giac BCD co:
AB = CD
BC = AD
BD chung
suy ra tam giac ABD = tam giac CDB (c.c.c)
d, ta co goc BAC = goc ACD (phan a)
Ma hai goc nay o vi tri so le trong bang nhau nen AB// CD.
Lai co goc CBD = goc ADB (phan c)
Ma hai goc nay o vi tri so le trong bang nhau nen BC//AD.

E A F B O C D Hình vẽ hơi xấu :V 1 2
a,Xét \(\Delta AOB\)và \(\Delta COD\)có :
\(OC=OA\)(gt)
\(OD=OB\)(gt)
\(O_1=O_2\)(đối đỉnh)
\(=>\Delta AOB=\Delta COD\left(c-g-c\right)\)
b,Ta có :\(DCO=BAO\)(cm câu a)
Do 2 góc này ở vị trí so le trong và bằng nhau
\(=>AB//CD\)
Xét \(\Delta DAO\)và \(\Delta BCO\)có :
\(OC=OA\)(gt)
\(OB=OD\)(gt)
\(COB=AOD\)(đối đỉnh)
\(=>\Delta DAO=\Delta BCO\left(c-g-c\right)\)
\(=>ODA=OBC\)(2 góc tương ứng)
Do 2 góc này ở vị trí so le trong và bằng nhau
\(=>DA//BC\)
Gọi giao điểm của CE và DO là H
giao điểm của AO và BE là G
Lại có \(DCO=BAO=>\frac{DCO}{2}=\frac{BAO}{2}=>FAG=HCO\)
\(FGA=CGE\)( đối đỉnh)
Xét \(\Delta AGF\)và \(\Delta CGE\):
\(AFG+FGA+FAG=GEC+CGE+ECG=180^0\)
Do \(FAG+FGA=CGE+ECG\)
\(=>CEG=AFG\)
Vì 2 góc này ở vị trí so le trong và bằng nhau
\(=>CE//AF\)
c,Ta có \(CEB=AFG\)(cm câu b)
Mà \(AFG=\frac{CAB+DBA}{2}=\frac{CAB+CDB}{2}\)(CDB = DBA Ta cm ở câu a)
\(=>CEB=\frac{CAB+CDB}{2}\left(đpcm\right)\)
O A B C D E F
a, xét ΔAOB và ΔCOD có : OA = OC (Gt)
OB = OD (gt)
^AOB = ^COD (đối đỉnh)
=> ΔAOB = ΔCAOD (c-g-c)
b, ΔAOB = ΔCAOD (Câu a)
=> ^CDO = ^OBA (định nghĩa) mà 2 góc này so le trong
=> DC // AB (Định lí)
xét ΔODA và ΔOBC có : OA = OC (gt)
OB = OD (gt)
^DOA = ^BOC (đối đỉnh)
=> ΔODA = ΔOBC (c-g-c)
=> ^ADO = ^OBC (đn) mà 2 góc này so le trong
=> AD // BC (định lí)
ΔAOB = ΔCOD (câu a)
=> ^DCO = ^OAB (định nghĩa)
CE là phân giác của ^DCO (gt) => ^ECO = ^DCO : 2 (tính chất)
AF là phân giác của ^OAB (gt) => ^OAF = ^OAB : 2 (tính chất)
=> ^ECO = ^OAF mà 2 góc này so le trong
=> CE // AF (định lí)
c, mjnh không biết làm

*Tự vẽ hình
a) Xét tam giác MAB và MDC có :
MA=MD(GT)
BM=CM(GT)
\(\widehat{BMA}=\widehat{DMC}\left(đđ\right)\)
=> Tam giác MAB=MDC ( c.g.c )
b) Mình nghĩ đề bài sửa thành CM AB//CD thì có vẻ đúng hơn
Có : Tam giác MAB=MDC (cmt)
=> \(\widehat{BAD}=\widehat{ADC}\)
Mà 2 góc này ở vị trí so le trong
=> AB//CD
- Xét tam giác ABD và CDA có :
AD-cạnh chung
\(\widehat{ADC}=\widehat{DAB}\left(tgMAB=MDC\right)\)
AB=BC(tgMAB=MDC)
=> 2 tam giác này bằng nhau
c) Vâng, như đề bài thì chúng ta đã có tam giác ABC vuông tại A nên khỏi cần chứng minh đâu :)
#Hoctot

a. Xét ΔOADvà ΔOCB:
Ta có: ˆO góc chung
OC=OA
CD=AB (OC=OA và OD=OB)
Vậy ΔOAD = ΔOCB (c.g.c)
Vậy ˆODA=ˆOBC (góc tương ứng)
Xét ΔABC và ΔCDA:
Ta có:
AC cạnh chung
ˆODA=ˆOBC
CD=AB (OC=OA và OD=OB)
Vậy ΔABC = ΔCDA(g.c.g)

Ta có hình vẽ:
a/ Xét tam giác AMD và tam giác CMB có
AM = MC (GT)
\(\widehat{AMD}\)=\(\widehat{CMB}\) (đối đỉnh)
MD = MB (GT)
Vậy tam giác AMD = tam giác CMB (c.g.c)
b/ Ta có: tam giác AMB = tam giác CMB (câu a)
=> \(\widehat{BCM}\)= \(\widehat{MAD}\)
Mà góc BCM; MAD ở vị trí so le trong
=> AD // BC (đpcm)
c/ Xét tam giác ABC và tam giác CDA có:
AC: cạnh chung
AD = BC (vì tam giác AMD = tam giác CMB)
\(\widehat{BCM}\)=\(\widehat{MAD}\)
Vậy tam giác ABC = tam giác CDA (c.g.c)
d/ Ta có: tam giác ABC = tam giác CDA (câu c)
=> \(\widehat{BAC}\) =\(\widehat{ACD}\)
Mà góc BAC; ACD ở vị trí so le trong
=> AB // CD (đpcm)