Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

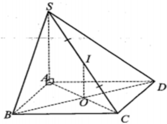
Gọi I là trung điểm AD \(\Rightarrow SI\perp AD\Rightarrow SI\left(ABCD\right)\Rightarrow d\left(I;\left(ABCD\right)\right)=SI\)
Ta có \(SM\cap\left(ABCD\right)=\left\{B\right\}\) và \(\frac{SB}{MB}=2\) nên \(d\left(M;\left(ABCD\right)\right)=\frac{1}{2}d\left(I;\left(ABCD\right)\right)=\frac{1}{2}SI=\frac{1}{2}\cdot\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{4}\)
\(S_{CNP}=\frac{1}{2}\cdot CN\cdot CP=\frac{1}{2}\cdot\frac{1}{2}CD\cdot\frac{1}{2}\cdot BC=\frac{a^2}{8}\)
\(V_{M.CNP}=\frac{1}{3}\cdot d\left(M;\left(ABCD\right)\right)\cdot S_{CNP}=\frac{a^3\sqrt{3}}{96}\)

Khá là dài, mình tìm ra được bằng \(\dfrac{3\sqrt3}{64}a^3\)

Chọn B.
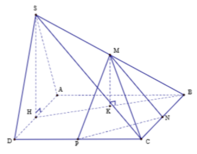
Gọi H là trung điểm của cạnh AD. Do tam giác SAD đều nên SH ⊥ AD
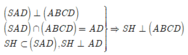
Gọi K là trung điểm của HB => MK//SH
Do đó: MK ⊥ ABCD => MK ⊥ (CNP).
Vậy MK là chiều cao của khối tứ diện CMNP.
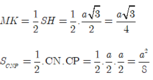
Thể tích khối tứ diện CMNP là
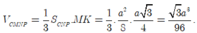
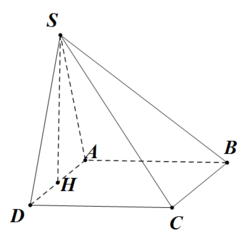

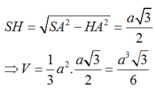





Gọi H là trung điểm AD \(\Rightarrow SH\perp\left(ABCD\right)\)
\(SH=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
Qua M kẻ đường thẳng song song AC cắt AD kéo dài tại E
\(\Rightarrow AC||\left(SME\right)\Rightarrow d\left(AC;SM\right)=d\left(AC;\left(SME\right)\right)=d\left(A;\left(SME\right)\right)\)
\(AE=\dfrac{1}{2}EH\Rightarrow d\left(A;\left(SME\right)\right)=\dfrac{1}{2}d\left(H;\left(SME\right)\right)\)
Các tam giác AHM và AEM vuông cân tại A \(\Rightarrow\Delta EHM\) vuông cân tại M
\(\Rightarrow EM\perp HM\Rightarrow EM\perp\left(SHM\right)\)
Từ H kẻ \(HK\perp SM\Rightarrow HK\perp\left(SME\right)\)
\(\Rightarrow HK=d\left(H;\left(SME\right)\right)\)
\(MH=AH\sqrt{2}=\dfrac{a\sqrt{2}}{2}\)
Áp dụng hệ thức lượng: \(\dfrac{1}{HK^2}=\dfrac{1}{SH^2}+\dfrac{1}{MH^2}=\dfrac{10}{3a^2}\Rightarrow HK=\dfrac{a\sqrt{30}}{10}\)
\(\Rightarrow d\left(SM;AC\right)=\dfrac{1}{2}HK=\dfrac{a\sqrt{30}}{20}\)