
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

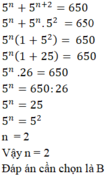

\(\dfrac{625}{5^n}\)=5
=>\(\dfrac{5^4}{5^n}\) =5
=>\(5^4\) :\(5^n\) = 5
=>\(5^{4-n}\) =\(5^1\)
=>4\(-\)n=1
=>n=4-1
=>n=3

2n-1:2=256
2n-1=512=29=>n-1=9=>n=10
5n+5n-2=650
5n-2(25+1)=650=>5n-2=25=52
=>n-2=2=>n=4

a)
\(2^{n-1}:2=256\)
\(\Rightarrow2^{n-1}:2=2^8\)
\(\Rightarrow2^{n-1}=2^9\)
\(\Rightarrow n-1=9\)
\(\Rightarrow n=10\)
b)
\(5^n+5^{n-2}=650\)
\(\Rightarrow5^n+5^n:5^2=650\)
\(\Rightarrow5^n+5^n:25=650\)
\(\Rightarrow5^n+5^n.\dfrac{1}{25}=650\)
\(\Rightarrow5^n.\left(1+\dfrac{1}{25}\right)=650\)
\(\Rightarrow5^n.\dfrac{26}{25}=650\)
\(\Rightarrow5^n=625\)
\(\Rightarrow5^n=5^4\)
\(\Rightarrow n=4\)
c)
\(2^{n-3}+2^{n+1}=136\)
\(\Rightarrow2^n.\dfrac{1}{2^3}+2^n.2=136\)
\(\Rightarrow2^n.\left(\dfrac{1}{8}+2\right)=136\)
\(\Rightarrow2^n.\dfrac{17}{8}=136\)
\(\Rightarrow2^n=64\)
\(\Rightarrow2^n=2^6\)
\(\Rightarrow n=6\)

a)
\(\left(\frac{1}{3}\right)^n\cdot27^n=3^n\)
\(\Rightarrow\left(\frac{1}{3}\cdot27\right)^n=3^n\)
\(\Rightarrow9^n=3^n\)
\(\Rightarrow\left(3^2\right)^n=3^n\)
\(\Rightarrow3^{2n}=3^n\)
\(\Rightarrow2n=n\)
\(\Leftrightarrow n=0\)
Vậy \(n=0\)
d) Ta có:
\(6^{3-n}=216\)
\(\Rightarrow6^{3-n}=6^3\)
\(\Rightarrow3-n=3\)
\(\Rightarrow n=3-3\)
\(\Rightarrow n=0\)
Vậy \(n=0\)\(\text{ }\)

a) \(\left(\frac{1}{3}\right)^n=\frac{1}{27}\)
\(\left(\frac{1}{3}\right)^n=\left(\frac{1}{3}\right)^3\)
\(\Rightarrow n=3\)
b) \(\left(\frac{3}{5}\right)^n=\frac{81}{625}\)
\(\left(\frac{3}{5}\right)^n=\left(\frac{3}{5}\right)^4\)
\(\Rightarrow n=4\)
c) \(3^n\cdot2^n=36\)
\(\left(3\cdot2\right)^n=36\)
\(6^n=6^2\)
\(\Rightarrow n=2\)
d) \(\frac{2^n}{3^n}=\frac{8}{27}\)
\(\left(\frac{2}{3}\right)^n=\left(\frac{2}{3}\right)^3\)
\(\Rightarrow n=3\)

Bài 2:
1: \(5^n+5^{n+2}=650\)
\(\Leftrightarrow5^n\cdot26=650\)
\(\Leftrightarrow5^n=25\)
hay x=2
2: \(32^{-n}\cdot16^n=1024\)
\(\Leftrightarrow\dfrac{1}{32^n}\cdot16^n=1024\)
\(\Leftrightarrow\left(\dfrac{1}{2}\right)^n=1024\)
hay n=-10
13: \(9\cdot27^n=3^5\)
\(\Leftrightarrow3^{3n}=3^5:3^2=3^3\)
=>3n=3
hay n=1

Đặt \(A=2.2^2+3.2^3+...+n.2^n\)
\(\Rightarrow2A=2.2^3+3.2^4+...+n.2^{n+1}\)
\(\Rightarrow A-2A=\)\(2.2^2+3.2^3+...+n.2^n\)\(-2.2^3-3.2^4-...-n.2^{n+1}\)
\(\Rightarrow-A=2.2^2+2^3+2^4+...+2^n-n.2^{n+1}\)
\(\Rightarrow-A=2^2+\left(2^2+2^3+2^4+...+2^{n+1}\right)-\left(n+1\right).2^{n+1}\)
\(\Rightarrow A=-2^2-\left(2^2+2^3+2^4+...+2^{n+1}\right)+\left(n+1\right).2^{n+1}\)
Đặt \(K=\left(2^2+2^3+2^4+...+2^{n+1}\right)\)
\(2K=\left(2^3+2^4+2^5+...+2^{n+2}\right)\)
\(2K-K=\left(2^3+2^4+2^5+...+2^{n+2}\right)\)\(-\left(2^2+2^3+2^4+...+2^{n+1}\right)\)
\(K=2^{n+2}-2^2\)
\(\Rightarrow A=-2^2-2^{n+2}+2^2+\left(n+1\right).2^{n+1}\)
\(\Rightarrow A=\left(n+1\right).2^{n+1}-2^{n+2}\)
\(\Rightarrow A=2^{n+1}\left(n+1-2\right)\)
\(\Rightarrow A=2^{n+1}\left(n-1\right)=2^{n+5}\Rightarrow2^4=n-1\Rightarrow n=17\)

\(\left(\frac{1}{2}\right)^n=\left(\frac{1}{8}\right)^5\)
\(\left(\frac{1}{2}\right)^n=\left(\frac{1^3}{2^3}\right)^5\)
\(\left(\frac{1}{2}\right)^n=\left[\left(\frac{1}{2}\right)^3\right]^5\)
\(\left(\frac{1}{2}\right)^n=\left(\frac{1}{2}\right)^{15}\)
n = 15
\(\left(\frac{1}{2}\right)^n=\left(\frac{1}{8}\right)^5\)
\(\Rightarrow\left(\frac{1}{2}\right)^n=\left(\frac{1}{2}\right)^{3.5}\)
\(\Rightarrow\left(\frac{1}{2}\right)^n=\left(\frac{1}{2}\right)^{15}\)
\(\Rightarrow n=15\)
Vậy n = 15

x+y=-2
Áp dụng t/c dãy tỉ số = nhau ta có
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y}{3+4}=\frac{-2}{7}\)
Suy ra x=\(\frac{-6}{7}\)
y=\(\frac{-8}{7}\)
z= thay vào dãy tỉ số tính hok tốt