
CM
Cao Minh Tâm
23 tháng 2 2017
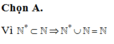
Đúng(0)